X3DNA-DSSR: a resource for structural bioinformatics of nucleic acids
(An NIGMS National Resource supported by NIH grant R24GM153869)

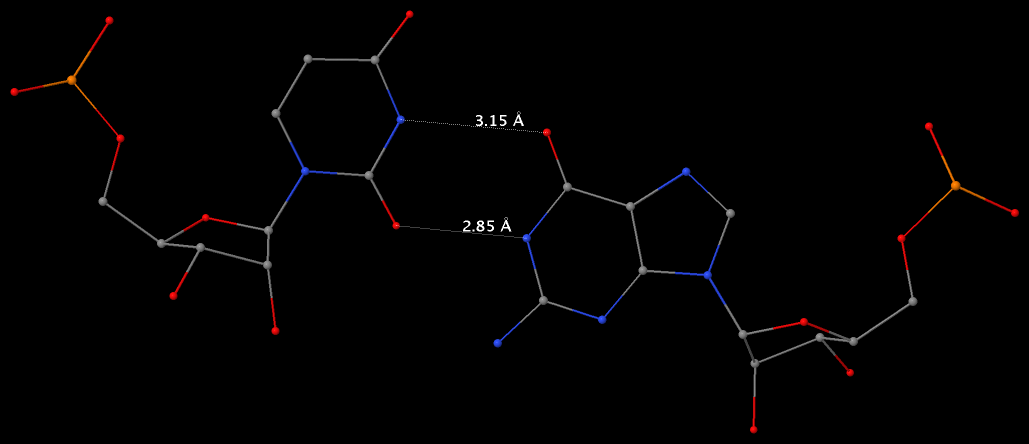
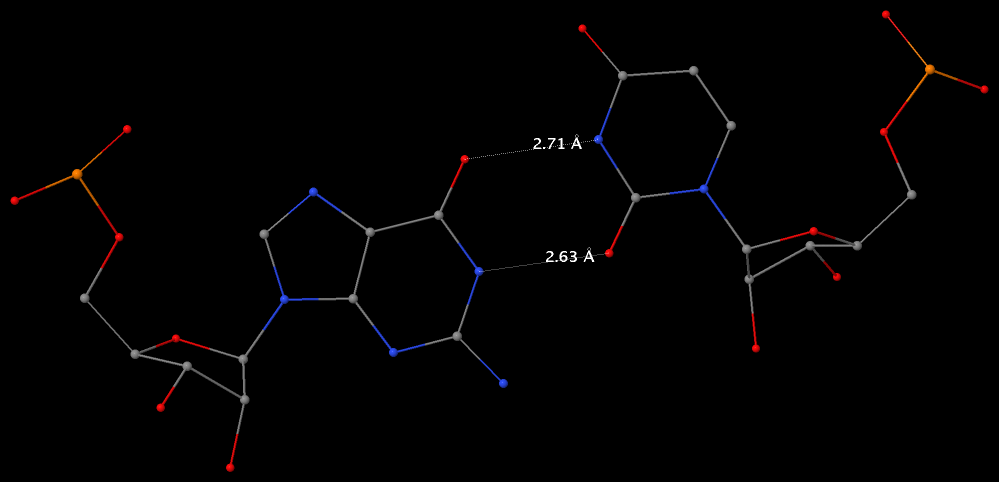
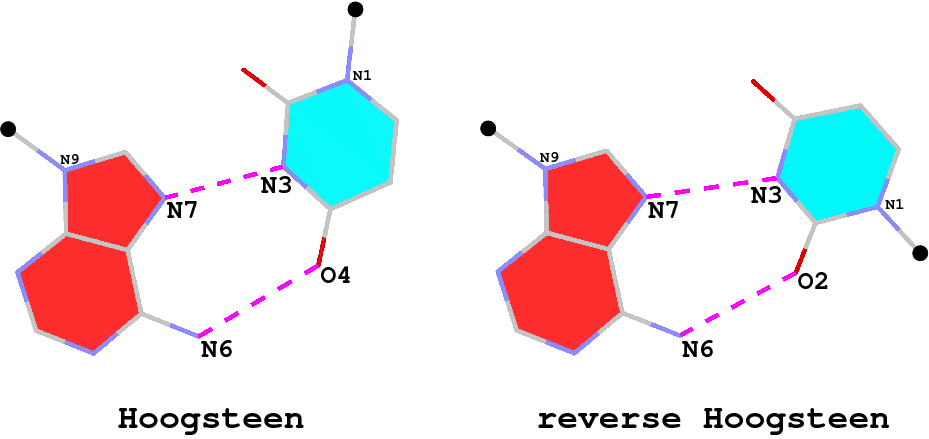
The A·U (or A·T) Hoogsteen pair is a well-known type of base pair (bp), named after the scientist who discovered it. As shown in the Figure below (left), in the Hoogsteen bp scheme, adenine uses its N7 (acceptor) and N6 (donor) atoms at the major groove edge to form two H-bonds with the N3 (donor) and O4 (acceptor) atoms from uracil, respectively. Interestingly, if the uracil base ring is flipped around the N7(A)…N3(U) H-bond by 180 degrees, N6(A) now forms an H-bond with O2(U), i.e., N6(A)…O2(U): this pairing scheme is called the reverse Hoogsteen bp (right).

I first knew about the Hoogsteen bp from Saenger’s book titled “Principles of Nucleic Acid Structure”. My knowledge of the Hoogsteen bp deepened as I tried to categorize different types of bps, especially in RNA-containing structures, in a consistent and rigorous computational framework. Thus, in the 3DNA NAR03 publication, we discussed specifically the bp (M+N type) and compared it with the A·U Watson-Crick bp (M–N type), as shown in the Figure below:

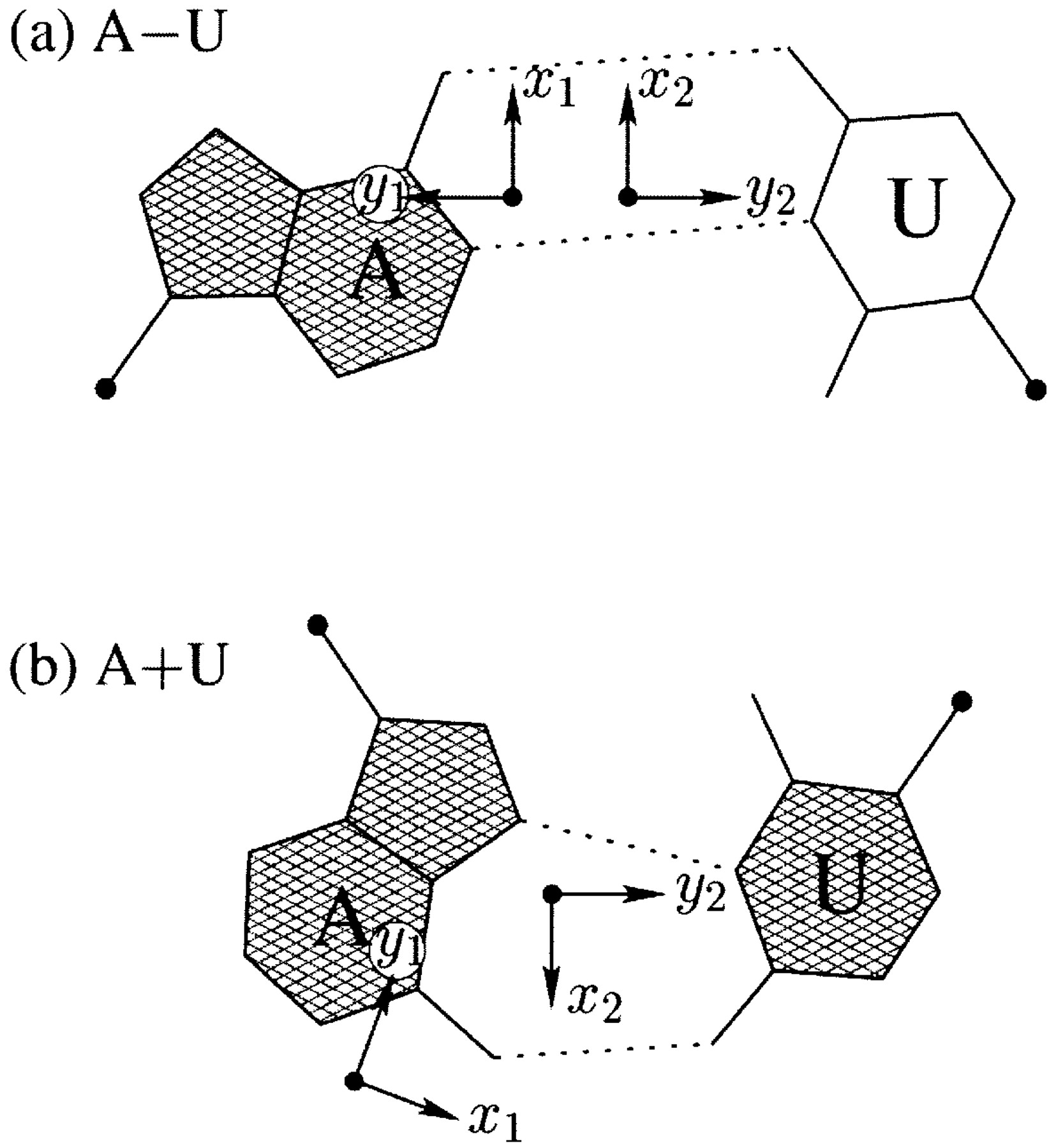
Antiparallel and parallel combinations of adenine (A) and uracil (U) base pair ‘faces’: (a) the antiparallel Watson–Crick A–U pair with opposing faces (shaded versus unshaded) and a 1.5 Å Stretch introduced to separate the two base reference frames; (b) the parallel Hoogsteen A+U pair with base pair faces of the same sense. Black dots on bases denote the C1′ atoms on the attached sugars.

However, only recently did I read the two original publications by Hoogsteen:

• The two-page long preliminary report, titled The structure of crystals containing a hydrogen-bonded complex of 1-methylthymine and 9-methyladenine [Acta Cryst. (1959). 12, pp.822-3]. It contains only a single reference, i.e. the 1953 Watson-Crick DNA structure Nature paper. Reading carefully through the two pages, I know why Hoogsteen used the methylated derivatives of thymine and adenine, and how the failed initial interpretation of the experimental “vector-density map” based on the Watson-Crick A-T bp led to the discovery of the new base-pairing scheme:

The fact that the first trial structure could not be refined led to a more critical scrutiny of the generalized projection and a greater emphasis on the significance of certain spurious peaks and on relatively large variations in the heights of peaks that were assumed to represent atoms. The correct structure was finally discovered by changing the positions of a few atoms in the 9-methyladenine portion of the asymmetric unit.

• The more extensive account of the Hoogsteen bp story, titled The Crystal and Molecular Structure of a Hydrogen-Bonded Complex Between 1-Methylthymine and 9-Methyladenine [Acta Cryst. (1963) 16, pp907-16].

I enjoyed reading these two papers a lot. More generally, I like such focused articles where authors get directly to a point and addressed it thoroughly and clearly.

As a side note, the term Hoogsteen “edge” appears frequently in nowaday’s publications of RNA structures: in the Leontis-Westhof bp classification scheme, this term simply means the major groove edge in what would be a Watson-Crick bp geometry.

3DNA, following SCHNArP, uses the alchemy file format for the schematic base-pair rectangular block representation. Alchemy is a simple molecular file format, suitable for chemical compounds by specifying atom positions and bond linkages explicitly. By checking a sample alchemy file (here for drug aspirin), scientists with chemistry knowledge should have little problem in figuring out what each field means. As it happens, the 3DNA alchemy representation of the base-pair rectangular block is much simpler than that of a typical chemical compound (e.g., aspirin). No different partial atomic charges or atom types, no distinction between single-, double- or aromatic bond types, the base-pair block can be specified with uniform pseudo-atoms (nodes) and pseudo-bonds (edges). Apart from being simple, alchemy was one of the common file formats supported by RasMol — that’s the pragmatic reason why I adopted the format in SCHNArP and 3DNA.

Over the years, 3DNA has been continuously using the alchemy format for base and base-pair rectangular blocks. It forms the basis of the Calladine-Drew style schematic representation images in PostScript (.eps), Xfig (.fig) and Raster3d (.r3d) formats. However, outside 3DNA, the alchemy format is not widely supported by popular molecular graphics programs, including RasMol, Jmol and PyMOL:

• RasMol v2.6.4, from Roger Sayle (the original author of RasMol), is mostly fine, except that the -noconnect option should be specified. As noted in the 3DNA Nature Protocols (2008) paper, The option ‘-noconnect’ makes sure that RasMol uses only the linkage information specified in the Alchemy file (by setting the CalcBondsFlag to false). … The … Alchemy files [can] contain explicitly specified coordinate axes, which would interfere with the default bond-calculation algorithm in RasMol.
• RasMol v2.7.x has a bug in displaying alchemy files.
• Jmol begins to support the alchemy format as of 11.7.18 (December 2008), following my request [see initial discussion and follow-up].
• PyMOL does not recognize the alchemy format.

To make the schematic base-pair rectangular block representation more broadly accessible, I have recently added the -mol option to alc2img in 3DNA v2.1 to readily convert an alchemy file to the well-documented and widely supported MDL molfile format. The usage is very simple — take the standard base-pair rectangular block file (Block_BP.alc) as an example, the conversion can be performed as below:

alc2img -mol Block_BP.alc Block_BP.mol
alc2img -molv3000 Block_BP.alc Block_BP_v3000.mol

Note the followings:

• By default, the -mol option converts alchemy to V2000 molfile format. However, if the number of atoms/bonds is greater then 999, the extended V3000 molfile format is used.
• The V3000 molfile format can be explicitly specified with -molv3000 (or -mol3), as shown above.
• Only V2000 molfile is consistently supported by RasMol, Jmol and PyMOL. On the other hand, while Jmol recognizes V3000 molfile, RasMol and PyMOL do not.
• For reference, the three files — Block_BP.alc, Block_BP.mol, and Block_BP_v3000.mol — are enclosed below.

Content of ‘Block_BP.alc’

   12 ATOMS,    12 BONDS
    1 N      -2.2500   5.0000   0.2500
    2 N      -2.2500  -5.0000   0.2500
    3 N      -2.2500  -5.0000  -0.2500
    4 N      -2.2500   5.0000  -0.2500
    5 C       2.2500   5.0000   0.2500
    6 C       2.2500  -5.0000   0.2500
    7 C       2.2500  -5.0000  -0.2500
    8 C       2.2500   5.0000  -0.2500
    9 C      -2.2500   5.0000   0.2500
   10 C      -2.2500  -5.0000   0.2500
   11 C      -2.2500  -5.0000  -0.2500
   12 C      -2.2500   5.0000  -0.2500
    1     1     2
    2     2     3
    3     3     4
    4     4     1
    5     5     6
    6     6     7
    7     7     8
    8     5     8
    9     9     5
   10    10     6
   11    11     7
   12    12     8

Content of ‘Block_BP.mol’ (V2000)

Block_BP.alc
XL 3DNAv2 
Converted from Alchemy format: Thu May  3 23:35:20 2012
 12 12  0     0  0              1 V2000
   -2.2500    5.0000    0.2500 N   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500   -5.0000    0.2500 N   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500   -5.0000   -0.2500 N   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500    5.0000   -0.2500 N   0  0  0  0  0  0  0  0  0  0  0  0
    2.2500    5.0000    0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
    2.2500   -5.0000    0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
    2.2500   -5.0000   -0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
    2.2500    5.0000   -0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500    5.0000    0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500   -5.0000    0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500   -5.0000   -0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
   -2.2500    5.0000   -0.2500 C   0  0  0  0  0  0  0  0  0  0  0  0
  1  2  1  0  0  0
  2  3  1  0  0  0
  3  4  1  0  0  0
  4  1  1  0  0  0
  5  6  1  0  0  0
  6  7  1  0  0  0
  7  8  1  0  0  0
  5  8  1  0  0  0
  9  5  1  0  0  0
 10  6  1  0  0  0
 11  7  1  0  0  0
 12  8  1  0  0  0
M END

Content of ‘Block_BP_v3000.mol’ (V3000)

Block_BP.alc
XL 3DNAv2 
Converted from Alchemy format: Thu May  3 23:22:04 2012
  0  0  0     0  0            999 V3000
M  V30 BEGIN CTAB
M  V30 COUNTS    12    12 0 0 0
M  V30 BEGIN ATOM
M  V30     1 N     -2.2500     5.0000     0.2500 0
M  V30     2 N     -2.2500    -5.0000     0.2500 0
M  V30     3 N     -2.2500    -5.0000    -0.2500 0
M  V30     4 N     -2.2500     5.0000    -0.2500 0
M  V30     5 C      2.2500     5.0000     0.2500 0
M  V30     6 C      2.2500    -5.0000     0.2500 0
M  V30     7 C      2.2500    -5.0000    -0.2500 0
M  V30     8 C      2.2500     5.0000    -0.2500 0
M  V30     9 C     -2.2500     5.0000     0.2500 0
M  V30    10 C     -2.2500    -5.0000     0.2500 0
M  V30    11 C     -2.2500    -5.0000    -0.2500 0
M  V30    12 C     -2.2500     5.0000    -0.2500 0
M  V30 END ATOM
M  V30 BEGIN BOND
M  V30     1 1    1    2
M  V30     2 1    2    3
M  V30     3 1    3    4
M  V30     4 1    4    1
M  V30     5 1    5    6
M  V30     6 1    6    7
M  V30     7 1    7    8
M  V30     8 1    5    8
M  V30     9 1    9    5
M  V30    10 1   10    6
M  V30    11 1   11    7
M  V30    12 1   12    8
M  V30 END BOND
M  V30 END CTAB
M END

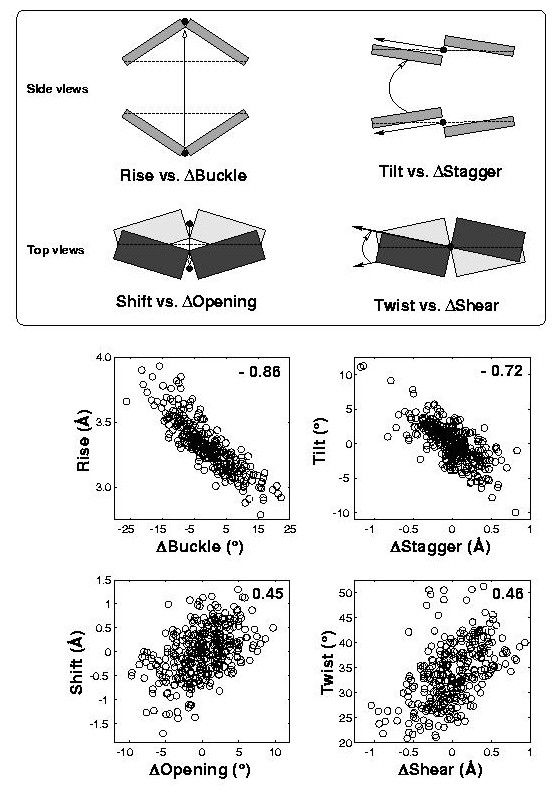
In the standard base reference frame report, a whole section is devoted to the discussion of intrinsic correlations between base-pair and dimer step parameters (see figure below). Among the four sets of associations, the effect of Δbuckle (difference in consecutive base-pair buckles) on rise is most noticeable and easiest to understand. The Δshear vs. twist relationship is similarly significant, due to its close connection to the wobble G–T/G–U pair; yet the concept is less comprehensible, especially to occasional 3DNA users. This post aims to address the issue of how Δshear effects twist.

Under the standard base reference frame used in 3DNA, the wobble base-pair has a ~2.0 Å shear: the displacement is positive for U–G, and negative for G–U [see figure below, examples selected from 5S rRNA (chain 9) U82–G100 and G83–U99 of the Haloarcula marismortui large ribosomal subunit, PDB id: 1jj2].

As noted in the section “treatment of non-Watson–Crick base pairing motifs” of the 3DNA Nucleic Acids Research paper (2003), “Large Shear of the G–U wobble base pair influences the calculated but not the ‘observed’ Twist. The 3DNA numerical values of Twist [of the C7G8·U12G13 and G8C9·G11U12 dimer steps of the Escherichia coli tRNA^Asp x-ray crystal structure (PDB id: 485d)], 20° (top) and 43° (bottom), differ from the visualization of nearly equivalent Twist suggested by the angle between successive C1′···C1′ vectors (finely dotted lines).”

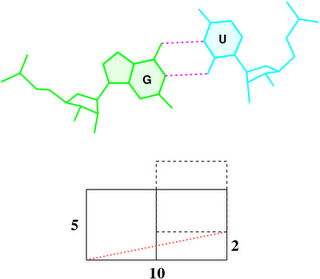
To make it clear why that’s the case, the figure below shows a G–U wobble pair in atomic representation (top), and a schematic base pair rectangular block of dimension 10×5 (Å, bottom). A shear of –2 Å moves U upwards, as outlined by the dashed rectangle, and causes a ‘misalignment’ of 11.3° between the C1′···C1′ vector (red dotted line) and the base-centered mean y-axis (horizontal line):

atan2(2, 10) * 180 / pi = 11.3°

To a first order approximation, that is the difference in twist angle. So whenever a wobble pair is next to a normal Watson-Crick pair, there would be a ~11° “observed” discrepancy with 3DNA calculated twist angle. Moreover, when a G–U wobble is next to a U–G wobble pair or vice versa, the difference would be doubled to ~22°.

The blocview script in 3DNA has been created as a handy tool to effectively reveal key features of small to medium-sized nucleic acid structures. Specifically, the bloc part of the name means ‘block’, i.e., the rectangular block in Calladine-Drew style schematic representation to distinguish bases by size (larger purine vs. smaller pyrimidine), identity (red for A, yellow for C, green for G, and blue for T), and groove (minor edge in black). The view part stands for the most extended view, as defined by the principal axes of inertia. Implementation-wise, blocview calls several 3DNA utility programs and MolScript (for protein ribbons and nucleic acid backbone rods) to prepare the scenes, and then uses Raster3D (specifically, render) or PyMol to generate a PNG image.

The blocview script was originally written in Perl. As of 3DNA v2.1, I decided to switch the scripting language to Ruby for its consistent object-oriented style, succinct and flexible syntax. Previously available Perl scripts are now moved out of the default 3DNA executable directory $X3DNA/bin/ into $X3DNA/perl_scripts/. The blocview script has been re-written in Ruby and set as the default (at $X3DNA/bin/blocview); the original Perl version is renamed blocview.pl (at $X3DNA/perl_scripts/blocview.pl) to avoid confusion. The command line help message, available via blocview -h, is as below:

------------------------------------------------------------------------
Generate a schematic image which combines base block representation
with protein ribbon. The image has informative color coding for the
nucleic acid part and is set in the "best view" by default. Raster3D
(or PyMOL) and ImageMagick must be installed.

Usage:
        blocview [options] PDBFile
Examples:
        blocview -i 355d.png 355d.pdb
             # generate image '355d.png'; display 355d.png
Options:
------------------------------------------------------------------------
     --imgfile, -i <s>:   name of image file (default: blocview.png)
     --r3dfile, -r <s>:   name of .r3d file (default: blocview.r3d)
   --dpi-pymol, -d <i>:   create PyMOL ray-traced image at specific DPI
       --scale, -s <f>:   set scale factor (for 'render' of Raster3D)
        --xrot, -x <f>:   rotation angle about x-axis
        --yrot, -y <f>:   rotation angle about y-axis
        --zrot, -z <f>:   rotation angle about z-axis
        --original, -o:   use original coordinates
  --ball-and-stick, -b:   get a ball-and-stick image
     --p-base-ring, -c:   use only P and base ring atoms
           --no-ds, -n:   do not show double-helix ribbon
         --protein, -p:   set best view based on protein atoms
             --all, -a:   set best view based on all atoms
         --version, -v:   Print version and exit
            --help, -h:   Show this message

Using the x-ray crystal structure of d(GGCCAATTGG) complexed with netropsin (1z8v) in the minor groove as an example, the command to run is as follows:

blocview -i 1z8v.png 1z8v.pdb
# The following two forms are also fine
#     blocview --imgfile 1z8v.png 1z8v.pdb
#     blocview --imgfile=1z8v.png 1z8v.pdb
# The Perl version can be run like this:
#     $X3DNA/perl_scripts/blocview.pl -i=1z8v.png 1z8v.pdb 

The image, named 1z8v.png, is shown below. Note that it is generated automatically from the PDB-formatted data file 1z8v.pdb. In this representation, one can see clearly that there are two unpaired Gs (green block) at each 5′-end of the two DNA chains (red and yellow rods), and a drug molecule (ball-and-stick) binds in the minor groove (black edge of the rectangular blocks). Moreover, the deformation in propeller and buckle is obvious in this schematic presentation.

Over the years, blocview-generated images have been used in NDB for virtually all nucleic acid structures (see for example, the NDB atlas gallery for x-ray drug-DNA complexes). It’s worth noting that such simple images have also be adopted by the RCSB PDB, prominently at the summary page, for nucleic acid containing structures (see PDB entry 1z8v). Given the effectiveness of blocview-generated schematic representation and its adoption by the NDB and PDB, I’m hopeful that blocview will be more widely used by the general DNA/RNA structure community. As always, I value user’s feedback in continuously refining the script.

One of 3DNA’s unique features is the simplified rectangular block representation of bases and base-pairs, as shown in the figure below. This type of schematic depiction was first made popular by Calladine and Drew (see their book titled Understanding DNA — The Molecule & How It Works), thus I usually call it the Calladine-Drew style representation.

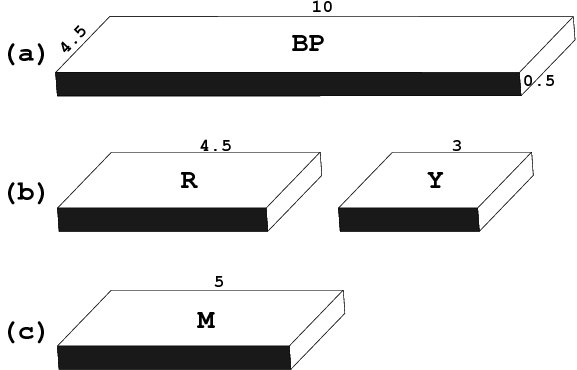
By default, a base-pair [BP, (a)] has dimensions of 10×4.5×0.5 (Å); a purine [R, (b) left] 4.5×4.5×0.5 (Å); a pyrimidine [Y, (b) right] 3×4.5×0.5 (Å); and a mean base [M, (c)], which is exactly half of the base-pair, 5×4.5×0.5 (Å).

The blocks are stored into separate files: Block_BP.alc, Block_R.alc, and Block_Y.alc for BP, R and Y respectively. To use M for R and Y (i.e., set R and Y to be of equal size), simple copy file Block_M.alc to overwrite Block_R.alc and Block_Y.alc in the current working directory for local effect, or the 3DNA installation directory ($X3DNA/config/) for global impact. These blocks are used in the rebuilding and visualization components of 3DNA.

Following SCHNArP, 3DNA uses alchemy, a simple chemical file format, to specify explicitly the nodes (atoms) and edges (bonds) of a rectangular block. Three file formats (alchemy, MDL molfile, and Tripos mol2), supported by RasMol v2.6 (the most popular molecular graphics visualization program in the 1990s), serve the purpose of specifying the rectangular block. I cannot recall exactly why I picked up -alchemy instead of -mdl and -mol2, perhaps because of its simplicity: I played around with sample alchemy files and came up with the alchemy rectangular block files used by SCHNArP, without much difficulty.

As an example, Block_BP.alc has the following content:

   12 ATOMS,    12 BONDS
    1 N      -2.2500   5.0000   0.2500
    2 N      -2.2500  -5.0000   0.2500
    3 N      -2.2500  -5.0000  -0.2500
    4 N      -2.2500   5.0000  -0.2500
    5 C       2.2500   5.0000   0.2500
    6 C       2.2500  -5.0000   0.2500
    7 C       2.2500  -5.0000  -0.2500
    8 C       2.2500   5.0000  -0.2500
    9 C      -2.2500   5.0000   0.2500
   10 C      -2.2500  -5.0000   0.2500
   11 C      -2.2500  -5.0000  -0.2500
   12 C      -2.2500   5.0000  -0.2500
    1     1     2
    2     2     3
    3     3     4
    4     4     1
    5     5     6
    6     6     7
    7     7     8
    8     5     8
    9     9     5
   10    10     6
   11    11     7
   12    12     8

Observant viewers may notice that nodes 1-4 are specified as nitrogens (N) which have exactly the same coordinates as 9-12 (carbons, C). This is a little trick to make RasMol display the minor groove edge in a different color (blue for N) than the other five sides of the rectangular (gray for C), as shown in the following figure:

Note that the rectangular is preset in the standard base reference frame. Thus the nodes have y-coordinates of +5 Å and -5 Å along the long edge of the base pair, and x-coordinates of +2.25 Å and -2.25 Å along the short edge.

As an extra bonus of storing the rectangular blocks in external alchemy text files, the dimensions of the blocks can be readily changed. For example, the thickness of a block (z-coordinates) can be easily increased from 0.5 to 1.0 Å to make it thicker. Moreover, the blocks do not need to be rectangular either — they can appear to be triangular blocks.

It’s worth noting that while extensively used in 3DNA for schematic representations, the alchemy format has largely become a legacy in cheminformatics/bioinformatics nowadays. Searching the internet, I cannot find the specification of the format. Moreover, the support of alchemy is quite limited and buggy in molecular graphics visualization programs most widely used today: PyMOL does not understand this format at all; RasMol v2.7 has a bug in interpreting it; only Jmol can properly read 3DNA base-pair rectangular block files in alchemy [see initial discussion and follow-up]. To resolve the issues associated with alchemy format, and thus to make 3DNA base-pair block schematics more widely available, I have recently added a converter in v2.1 to readily transform alchemy to MDL molfile, a format consistently supported by PyMOL, Jmol and RasMol. I’ll talk about this feature in another post.

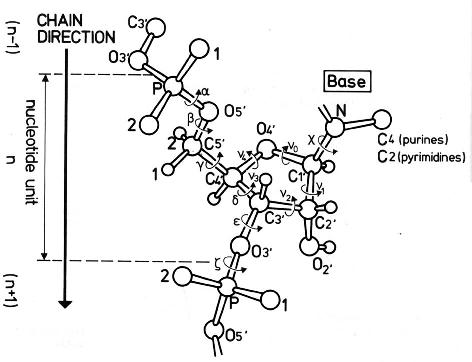
The conformation of the five-membered sugar ring in DNA/RNA structures can be characterized by the five consecutive endocyclic torsion angles (see Figure below), i.e.,

ν0: C4′-O4′-C1′-C2′
ν1: O4′-C1′-C2′-C3′
ν2: C1′-C2′-C3′-C4′
ν3: C2′-C3′-C4′-O4′
ν4: C3′-C4′-O4′-C1′

Due to the ring constraint, the conformation can be characterized approximately by 5-3=2 parameters. Using the concept of pseudorotation of the sugar ring, the two parameters are the amplitude (τ_m) and phase angle (P).

One set of widely used formula to convert the five torsion angles to the pseudorotation parameters is due to Altona & Sundaralingam (1972): Conformational Analysis of the Sugar Ring in Nucleosides and Nucleotides. A New Description Using the Concept of Pseudorotation [J. Am. Chem. Soc., 94(23), pp. 8205–8212]. The concept is easily illustrated with an example — here with the G4 sugar ring on chain A of the Dickerson dodecamer (1bna), using Octave/Matlab code:

# xyz coordinates of the G4 sugar ring on chain A of 1bna
# ATOM     63  C4'  DG A   4      21.393  16.960  18.505  1.00 53.00
# ATOM     64  O4'  DG A   4      20.353  17.952  18.496  1.00 38.79
# ATOM     65  C3'  DG A   4      21.264  16.229  17.176  1.00 56.72
# ATOM     67  C2'  DG A   4      20.793  17.368  16.288  1.00 40.81
# ATOM     68  C1'  DG A   4      19.716  17.901  17.218  1.00 30.52

# endocyclic torsion angles:
v0 = -26.7; v1 = 46.3; v2 = -47.1; v3 = 33.4; v4 = -4.4;
Pconst = sin(pi/5) + sin(pi/2.5);  # 1.5388
P0 = atan2(v4 + v1 - v3 - v0, 2.0 * v2 * Pconst); # 2.9034
tm = v2 / cos(P0)  # amplitude: 48.469
P = 180/pi * P0  # phase angle: 166.35 [P + 360 if P0 < 0]

The Altona & Sundaralingam (1972) pseudorotation parameters are what have been adopted in 3DNA. The Curves+ program, on the other hand, uses another set of formula due to Westhof & Sundaralingam (1983): A Method for the Analysis of Puckering Disorder in Five-Membered Rings: The Relative Mobilities of Furanose and Proline Rings and Their Effects on Polynucleotide and Polypeptide Backbone Flexibility. [J. Am. Chem. Soc., 105(4), pp. 970–976]. The two sets of formula — Altona & Sundaralingam (1972) and Westhof & Sundaralingam (1983) — give slightly different numerical values for the two pseudorotation parameters (see below).

Since Curves+ and 3DNA are currently the most commonly used programs for conformational analysis of nucleic acid structures, the subtle differences in these two pseudorotation parameters may cause confusions for users who use both programs. With the same G4 (on chain A of 1bna) sugar ring, here is the Octave/Matlab script showing how Curve+ calculates the pseudorotation parameters:

# xyz coordinates of the G4 sugar ring on chain A of 1bna
# endocyclic torsion angles, same as above
v0 = -26.7; v1 = 46.3; v2 = -47.1; v3 = 33.4; v4 = -4.4;

v = [v2, v3, v4, v0, v1]; # reorder them into vector v[]
A = 0; B = 0;
for i = 1:5
    t = 0.8 * pi * (i - 1);
    A += v(i) * cos(t);
    B += v(i) * sin(t);
end
A *= 0.4;   # -48.476
B *= -0.4;  # 11.516

tm = sqrt(A * A + B * B);  # 49.825

c = A/tm; s = B/tm;
P = atan2(s, c) * 180 / pi;  # 166.64

For this specific example, i.e., the G4 sugar ring on chain A of 1bna, the pseudorotation parameters as calculated by 3DNA following Altona & Sundaralingam (1972) and Curves+ following Westhof & Sundaralingam (1983) are as follows:

Needless to say, for the majority of cases like the one shown here, the differences are subtle; very few people would notice them or be bothered at all. For those who do care about such little details, however, this post shows where the discrepancies really come from.

In the field of nucleic acid structural analysis, it seems fair to say that Curves+ and 3DNA are nowadays the top two choices. To the best of my knowledge, these two programs are also the only ones that confirm to the standard base reference frame. Moreover, as noted in my previous post, Curves+ and 3DNA are “constructive competitors” with complementary functionality: Curves+ is unique in providing a curvilinear helical axis, a bending analysis, a full description of groove widths and depths and its seamless integration to the analysis of molecular dynamics trajectories, while 3DNA’s strength lies in its cohesrent approach combining analysis, rebuilding, and visualization into one package.

Given the complementarity between Curve+ and 3DNA, it makes sense to build a ‘bridge’ between the two so users can easily take advantage of both programs. Starting from 3DNA v1.5, find_pair has the -c option to generate input for Curves directly from a PDB file. Over the years, this option appears to have received little attention — at least, I am not aware of any literature reference to it. Now, the updated Curves+ program has introduced the new lib name list variable, among other changes. I have thus added the -curves+ option (abbreviation -c+) to find_pair to make its output compatible with Curves+.

As always, the point/process is best illustrated with an example — here with the Dickerson B-DNA dodecamer solved at high resolution by Williams et al. (PDB entry 355d).

find_pair -c+ 355d.pdb 355d-curves+.inp

The generated file 355d-curves+.inp has the following content:

&inp file=355d.pdb,
     lis=355d,
     fit=.t.,
     lib=/Users/xiangjun/Curves+/standard,
     isym=1,
&end
    2    1   -1    0    0
    1    2    3    4    5    6    7    8    9   10   11   12
   24   23   22   21   20   19   18   17   16   15   14   13

which can be fed into Curves+ as below,

Cur+ < 355d-curves+.inp

The four output files are: 355d.cda, 355d.lis, 355d_X.pdb and 355d_b.pdb.

Please note the followings:

• The environment variable CURVES_PLUS_STDLIB should be set, pointing to the directory where Curves+ is installed (containing files standard_b.lib and standard_s.lib). In the example above, CURVES_PLUS_STDLIB is set to /Users/xiangjun/Curves+.
• The find_pair -c+ option (currently) is applicable only to double helical DNA/RNA structures, the most common application scenario.
• The -c+ option ignores HETATM records, in accordance with Curves+ where proteins, water and HETATM are automatically removed at input. (see Curves+ user manual, section Input data)
• To run Cur+ < 355d-curves+.inp again in the same folder, the four output files must first be deleted (e.g., rm -f 355d.cda 355d.lis 355d_[Xb].pdb). This is best taken care of via a script.

Obviously, the nucleic acid structure community benefits the most to have both Curves+ and 3DNA at its disposal and be able to easily switch between them — hopefully, the find_pair -c+ option would serve as such a ‘bridge’.

From the very beginning, 3DNA calculates a set of nucleic acid backbone parameters, including the six main chain torsion angles (α, β, γ, δ, ε, and ζ) around the covalent bonds, χ about the glycosidic bond, and the sugar pucker (see figure below). For double helical structures, the standard analyze output (.out file) has a section for “Main chain and chi torsion angles,” and another dedicated to “Sugar conformational parameters”. Based on my experience/understanding, these two parts are well recognized and utlizied by 3DNA users. What has receive little attention (in spite of the several posts I’ve written on the topic), though, is 3DNA’s applicability to single-stranded (ss) RNA structures for the backbone torsions, among other parameters. Using the fully refined crystal structure of the Haloarcula marismortui large ribosomal subunit (PDB entry 1jj2) as an example, the procedure is below:

find_pair -s 1jj2.pdb 1jj2.nts
analyze 1jj2.nts
    # or the above two steps can be combined:
find_pair -s 1jj2.pdb stdout | analyze stdin
    # see output file '1jj2.outs'

In retrospect, the fact that 3DNA has been little used for RNA backbone conformational analysis is of no surprise:

• While base-pair parameters have different (oftentimes confusing) definitions, these backbone parameters are pretty “standard” — thus, for example, any program for DNA/RNA structural analysis would give the same numerical values for α or χ torsion angles.
• The two-step process as illustrated above is a bit awkward, and the torsions are “buried” among many other parameters.
• 3DNA is more directly “linked” (conceivably) to DNA base pairs than to RNA backbone.

So while adapting the Zp parameter for ss DNA/RNA structures in 3DNA v2.1, I also take this opportunity to add the -torsion option to analyze with the following handy features:

• Streamline the calculation by starting directly from a PDB file and output only backbone parameters. So the above example can be shortened to analyze -t=1jj2.tor 1jj2.pdb; the output file is named 1jj2.tor.
• Classify backbone into BI/BII conformation, and base χ into syn / anti.
• Add pseudo-torsions, and Zp and Dp as defined by Richardson et al.
• Handle pseudouridine sensibly, and work also for nucleic acid structure with only backbone atoms.
• Be easy to use, efficient and robust — it takes ~1 second to process the large ribosomal subunit 1jj2 (with 2876 nucleotides consisting of 23S rRNA and 5S rRNA) on my MacBook Air.

Overall, analyze -torsion is designed to be pragmatic and allows for automatic processing of all NDB entries or molecular dynamics trajectories. Given below is an excerpt of the three sections from an analyze -torsion run on 1jj2:

****************************************************************************
Main chain and chi torsion angles: 

Note: alpha:   O3'(i-1)-P-O5'-C5'
      beta:    P-O5'-C5'-C4'
      gamma:   O5'-C5'-C4'-C3'
      delta:   C5'-C4'-C3'-O3'
      epsilon: C4'-C3'-O3'-P(i+1)
      zeta:    C3'-O3'-P(i+1)-O5'(i+1)

      chi for pyrimidines(Y): O4'-C1'-N1-C2
          chi for purines(R): O4'-C1'-N9-C4

          If chi is in range [-90, +90], syn conformation
              otherwise, it is in anti conformation

          e-z: epsilon - zeta
              BI:  e-z = [-160, +20]
              BII: e-z = [+20, +200]

              base      chi         alpha    beta   gamma   delta  epsilon   zeta     e-z
   1 0:..10_:[..U]U   -62.5(syn)     ---     ---     56.2    74.0   142.2   -87.8  -130.1(BI) 
   2 0:..11_:[..A]A   171.5(anti)   173.2  -161.0   168.5    84.0  -112.1   -65.4   -46.7(BI) 
   3 0:..12_:[..U]U  -167.7(anti)   -70.7   168.4    53.0    78.5  -128.5   -46.4   -82.1(BI) 
   4 0:..13_:[..G]G  -172.5(anti)   -61.8   170.4    67.7    73.5  -166.7   -79.6   -87.1(BI) 
   5 0:..14_:[..C]C  -166.0(anti)   -73.0  -172.5    55.1    83.2  -143.3   -77.7   -65.6(BI) 
   6 0:..15_:[..C]C  -155.5(anti)   -60.9   174.1    47.3    80.3  -154.4   -71.2   -83.2(BI) 

****************************************************************************
Pseudo (virtual) eta/theta torsion angles:

Note: eta:    C4'(i-1)-P(i)-C4'(i)-P(i+1)
      theta:  P(i)-C4'(i)-P(i+1)-C4'(i+1)

      eta':   C1'(i-1)-P(i)-C1'(i)-P(i+1)
      theta': P(i)-C1'(i)-P(i+1)-C1'(i+1)

      eta":   Borg(i-1)-P(i)-Borg(i)-P(i+1)
      theta": P(i)-Borg(i)-P(i+1)-Borg(i+1)

              base      eta   theta    eta'  theta'    eta"  theta"
   1 0:..10_:[..U]U    ---     ---     ---     ---     ---     --- 
   2 0:..11_:[..A]A  -174.6  -129.7   177.0  -127.7  -157.5   -75.5
   3 0:..12_:[..U]U   149.1  -105.1   174.1  -101.2  -111.0   -69.4
   4 0:..13_:[..G]G   169.0  -172.5  -156.6  -169.2   -93.3  -137.1
   5 0:..14_:[..C]C   176.2  -143.4   179.6  -140.6  -144.6  -120.6
   6 0:..15_:[..C]C   165.0  -147.7   177.4  -146.8  -149.2  -121.7

****************************************************************************
Sugar conformational parameters: 

Note: v0: C4'-O4'-C1'-C2'
      v1: O4'-C1'-C2'-C3'
      v2: C1'-C2'-C3'-C4'
      v3: C2'-C3'-C4'-O4'
      v4: C3'-C4'-O4'-C1'

      tm: the amplitude of pucker
      P:  the phase angle of pseudorotation

      Zp: z-coordinate of the 3' phosphorus atom (P) expressed in the
            standard base reference frame; it's POSITIVE when P is on
            the +z-axis side (base in anti conformation); NEGATIVE if
            P is on the -z-axis side (base in syn conformation)
      Dp: perpendicular distance of the 3' P atom to the glycosydic bond
            [as per the MolProbity paper of Richardson et al. (2010)]

              base       v0      v1      v2      v3      v4     tm       P    Puckering    Zp      Dp
   1 0:..10_:[..U]U   -11.3   -15.4    34.5   -41.8    33.5    41.6    33.8    C3'-endo   -0.13    3.53
   2 0:..11_:[..A]A    11.4   -30.2    36.9   -31.5    12.6    36.9     1.2    C3'-endo    4.74    4.78
   3 0:..12_:[..U]U     3.6   -29.3    42.4   -41.3    23.8    43.6    13.9    C3'-endo    4.67    4.82
   4 0:..13_:[..G]G   -13.0   -17.8    39.8   -47.9    38.5    47.8    33.7    C3'-endo    4.45    4.46
   5 0:..14_:[..C]C     6.0   -28.4    38.9   -36.5    19.2    39.5    10.1    C3'-endo    4.57    4.70
   6 0:..15_:[..C]C     1.9   -26.4    39.6   -39.6    23.7    41.2    16.0    C3'-endo    4.32    4.61

Given the x-, y-, and z-coordinates of four points (a-b-c-d) in 3-dimensional (3D) space, how to calculate the torsion angle? Overall, this is a well-solved problem in structural biology and chemistry; one can find a description of torsion angle in many text books and on-line documents. The algorithm for its calculation is implementated in virtually every software package in computational structural biology and chemistry.

As basic as the concept is, however, it is important (based on my experience) to have a clear understanding of how torsion angle is defined in order to really get into the 3D world. Here is a worked example using Octave/Matlab of my simplified, geometry-based implementation of calculating torsion angle, including how to determine its sign. No theory or (complicated) mathematical formula, just a step-by-step illustration of how I solve this problem.

• Coordinates of four points are given in variable abcd:

abcd = [ 21.350  31.325  22.681
         22.409  31.286  21.483
         22.840  29.751  21.498
         23.543  29.175  22.594 ];

• Two auxiliary functions: norm_vec() to normalize a vector; get_orth_norm_vec() to get the orthogonal component (normalized) of a vector with reference to another vector, which should have already been normalized.

function ovec = norm_vec(vec)
    ovec = vec / norm(vec);
endfunction

function ovec = get_orth_norm_vec(vec, vref)
    temp = vec - vref * dot(vec, vref);
    ovec = norm_vec(temp);
endfunction

• Get three vectors: b_c is the normalized vector b→c; b_a_orth is the orthogonal component (normalized) of vector b→a with reference to b→c; c_d_orth is similarly defined, as the orthogonal component (normalized) of vector c→d with reference to b→c.

b_c = norm_vec(abcd(3, :) - abcd(2, :))
    % [0.2703158  -0.9627257   0.0094077]
b_a_orth = get_orth_norm_vec(abcd(1, :) - abcd(2, :), b_c)
    % [-0.62126  -0.16696   0.76561]
c_d_orth = get_orth_norm_vec(abcd(4, :) - abcd(3, :), b_c)
    % [0.41330   0.12486   0.90199]

• Now the torsion angle is defined as the angle between the two vectors, b_a_orth and c_d_orth, and can be easily calculated by their dot product. The sign of the torsion angle is determined by the relative orientation of the cross product of the same two vectors with reference to the middle vector b→c. Here they are in opposite direction, thus the torsion angle is negative.

angle_deg = acos(dot(b_a_orth, c_d_orth)) * 180 / pi  % 65.609
sign = dot(cross(b_a_orth, c_d_orth), b_c)  % -0.91075
if (sign < 0)
    ang_deg = -angle_deg  % -65.609
endif

A related concept is the so-called dihedral angle, or more generally the angle between two planes. As long as the normal vectors to the two corresponding planes are defined, the angle between them is easy to work out.

It’s worth noting that the helical twist angle in SCHNAaP and 3DNA is calculated similarly.