X3DNA-DSSR: a resource for structural bioinformatics of nucleic acids
(An NIGMS National Resource supported by NIH grant R24GM153869)

As of today (2012-09-16), the number of 3DNA forum registrations has reached 500! A quick browse of the ‘Statistics Center’ shows that over 80% of the registrations (400+) are after March 2012, when the new 3DNA homepage/forum were launched.

The sharp increase in registration is mostly due to the streamlined, web-based way to distribute the 3DNA software package. As far as I know, the number of 3DNA registrations/downloads in the past six months is significantly higher than that of 3DNA v2.0 for over three years. Equally importantly, I have been able to fixed every reported bug, addressed each feature request, and updated the 3DNA v2.1 distribution promptly.

I also feel confident to declare that up to now, the 3DNA Forum is spam free (at least to the extent I am aware). To this end, I’ve taken the following three measures:

• Installation of the SMF “Mod Stop Spammer”; as of this writing, it shows “3920 Spammers blocked up until today”.
• By using 3DNA-related verification questions. At its current setting, a user must answer correctly three of the ‘simple’ yet effective verification questions. Early on, I decided deliberately not to use CAPTCHA as an anti-spam means, based on my past experience.
• I’ve continuously monitored (new) registrations, and taken immediate actions against any suspicious registration. Due to the effectiveness of above two steps, so far I only have to manually handle just a few spam registrations. Nevertheless, it does illustrate the fact that no automatic method is perfect, and expert inspection is required to ensure desired results.

Overall, the new simplified way to distribute the 3DNA software package is working as intended; now users can easily access all distributed versions of 3DNA, and I can focus on support and further development of the software.

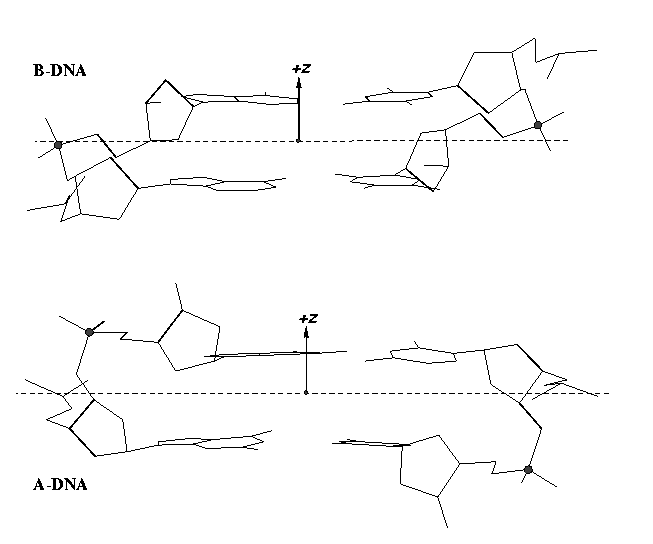
From v1.5 or even earlier on, 3DNA provides an automatic classification of a dinucleotide step into A-, B- or TA-DNA conformation. Figure 5 of the 2003 3DNA Nucleic Acids Research paper (NAR03) shows three sets of scatter plots — helical inclination and x‐displacement, dimer step Roll and Slide, and the projected phosphorus z coordinates Zp and Zp(h) — to differentiate the A-, B- and TA-DNA dinucleotide steps.

Among the criteria tested, the most discriminative ones are the projected phosphorus z coordinates, Zp in the middle step frame (see figure below), and Zp(h) defined similarly but in the middle helical frame.

Over the years, I have received many questions regarding the datasets used in generating Figure 5 of NAR03. Back in August 2006, a user asked for IDs of the TA-DNA structures — see DNA standards/statistics using 3DNA. In April 2007, another user requested the same TA-DNA dataset. Early this year, a user asked for 3DNA’s A-DNA definition. More recently, yet another user would like to ask about the DNA set used for the analysis that is presented in Fig 5. in the NAR 2003 paper.

I am glad to see that after nearly a decade of the NAR03 publication, the user community is still interested in knowing details in the work. So I decided to dig into my archive for the original data files and scripts used to generate Figure 5 of NAR03. It was not an easy journey; just releasing the data files and scripts is not enough, I’d like to verify that they work together as intended in today’s computing environment. Luckily, I am finally able to get to the bottom of the issues. The details are in the post Datasets and scripts for reproducing Figure 5 of the 3DNA NAR03 paper. The tarball file named 3DNA-NAR03-Fig5.tar.gz is available by clicking the link.

As noted in post Rectangular block expressed in MDL molfile format, I added the -mol option (in v2.1) to convert 3DNA’s native alchemy to the better-supported MDL molfile format, to make the characteristic schematic representations more widely accessible. Along the line, I have recently further augmented alc2img with the -pdb option to transform alchemy to the PDB format.

While the macromolecular PDB format is certainly not convenient for specifying linkage details of small molecules, it’s nevertheless the best-documented and by far the most widely supported than molfile or alchemy in currently available molecular viewers. For example, the PDB format is consistently supported in Jmol, PyMOL, RasMol, DeepView, and UCSF Chimera. Moreover, the PDB format does have the CONECT section to provide information on atomic connectivity:

The CONECT records specify connectivity between atoms for which coordinates are supplied. The connectivity is described using the atom serial number as shown in the entry. CONECT records are mandatory for HET groups (excluding water) and for other bonds not specified in the standard residue connectivity table.

The alc2img -pdb option takes advantage of the CONECT records and specifies all ‘bond’ linkages explicitly. The usage is very simple — take the standard base-pair rectangular block file (‘Block_BP.alc’) as an example, the conversion can be performed as below:

alc2img -pdb Block_BP.alc Block_BP.pdb

Content of ‘Block_BP.alc’

   12 ATOMS,    12 BONDS
    1 N      -2.2500   5.0000   0.2500
    2 N      -2.2500  -5.0000   0.2500
    3 N      -2.2500  -5.0000  -0.2500
    4 N      -2.2500   5.0000  -0.2500
    5 C       2.2500   5.0000   0.2500
    6 C       2.2500  -5.0000   0.2500
    7 C       2.2500  -5.0000  -0.2500
    8 C       2.2500   5.0000  -0.2500
    9 C      -2.2500   5.0000   0.2500
   10 C      -2.2500  -5.0000   0.2500
   11 C      -2.2500  -5.0000  -0.2500
   12 C      -2.2500   5.0000  -0.2500
    1     1     2
    2     2     3
    3     3     4
    4     4     1
    5     5     6
    6     6     7
    7     7     8
    8     5     8
    9     9     5
   10    10     6
   11    11     7
   12    12     8

Content of ‘Block_BP.pdb’

REMARK    3DNA v2.1 (c) 2012 Dr. Xiang-Jun Lu (http://x3dna.org)
HETATM    1  N   ALC A   1      -2.250   5.000   0.250  1.00  1.00           N  
HETATM    2  N   ALC A   1      -2.250  -5.000   0.250  1.00  1.00           N  
HETATM    3  N   ALC A   1      -2.250  -5.000  -0.250  1.00  1.00           N  
HETATM    4  N   ALC A   1      -2.250   5.000  -0.250  1.00  1.00           N  
HETATM    5  C   ALC A   1       2.250   5.000   0.250  1.00  1.00           C  
HETATM    6  C   ALC A   1       2.250  -5.000   0.250  1.00  1.00           C  
HETATM    7  C   ALC A   1       2.250  -5.000  -0.250  1.00  1.00           C  
HETATM    8  C   ALC A   1       2.250   5.000  -0.250  1.00  1.00           C  
HETATM    9  C   ALC A   1      -2.250   5.000   0.250  1.00  1.00           C  
HETATM   10  C   ALC A   1      -2.250  -5.000   0.250  1.00  1.00           C  
HETATM   11  C   ALC A   1      -2.250  -5.000  -0.250  1.00  1.00           C  
HETATM   12  C   ALC A   1      -2.250   5.000  -0.250  1.00  1.00           C  
CONECT    1    2    4                                                  
CONECT    2    1    3                                                  
CONECT    3    2    4                                                  
CONECT    4    1    3                                                  
CONECT    5    6    8    9                                             
CONECT    6    5    7   10                                             
CONECT    7    6    8   11                                             
CONECT    8    5    7   12                                             
CONECT    9    5                                                       
CONECT   10    6                                                       
CONECT   11    7                                                       
CONECT   12    8                                                       
END

From a pure structural perspective, the designation of the two strands in an anti-parallel DNA duplex is sort of arbitrary. Thus, for a given PDB file, let’s assume that the atomic coordinates of chain A (strand I) come before those of chain B (strand II). We can swap the order of the two chains as they appear in the PDB file, i.e., list first the atomic coordinates of chain B and then those of chain A.

Structurally, the two settings corresponding to exactly the same DNA molecule. As far as 3DNA goes, however, the different orderings do make a different in calculated parameters. Using the Dickerson B-DNA dodecamer CGCGAATTCGCG solved at high resolution (PDB entry 355d) as an example, running 3DNA find_pair and analyze on ‘355d.pdb’ gives the results (abbreviated) below:

find_pair 355d.pdb 355d.bps
    # contents of file '355d.bps':
------------------------------------------------------------------
355d.pdb
355d.out
    2         # duplex
   12         # number of base-pairs
    1    1    # explicit bp numbering/hetero atoms
    1   24  0 #    1 | ....>A:...1_:[.DC]C-----G[.DG]:..24_:B<....
    2   23  0 #    2 | ....>A:...2_:[.DG]G-----C[.DC]:..23_:B<....
    3   22  0 #    3 | ....>A:...3_:[.DC]C-----G[.DG]:..22_:B<....
    4   21  0 #    4 | ....>A:...4_:[.DG]G-----C[.DC]:..21_:B<....
    5   20  0 #    5 | ....>A:...5_:[.DA]A-----T[.DT]:..20_:B<....
    6   19  0 #    6 | ....>A:...6_:[.DA]A-----T[.DT]:..19_:B<....
    7   18  0 #    7 | ....>A:...7_:[.DT]T-----A[.DA]:..18_:B<....
    8   17  0 #    8 | ....>A:...8_:[.DT]T-----A[.DA]:..17_:B<....
    9   16  0 #    9 | ....>A:...9_:[.DC]C-----G[.DG]:..16_:B<....
   10   15  0 #   10 | ....>A:..10_:[.DG]G-----C[.DC]:..15_:B<....
   11   14  0 #   11 | ....>A:..11_:[.DC]C-----G[.DG]:..14_:B<....
   12   13  0 #   12 | ....>A:..12_:[.DG]G-----C[.DC]:..13_:B<....
------------------------------------------------------------------

analyze 355d.bps
    # generate output file '355d.out', with base-pair step parameters:
****************************************************************************
    step       Shift     Slide      Rise      Tilt      Roll     Twist
   1 CG/CG      0.09      0.04      3.20     -3.22      8.52     32.73
   2 GC/GC      0.50      0.67      3.69      2.85     -9.06     43.88
   3 CG/CG     -0.14      0.59      3.00      0.97     11.30     25.11
   4 GA/TC     -0.45     -0.14      3.39     -1.59      1.37     37.50
   5 AA/TT      0.17     -0.33      3.30     -0.33      0.46     37.52
   6 AT/AT     -0.01     -0.60      3.22     -0.31     -2.67     32.40
   7 TT/AA     -0.08     -0.40      3.22      1.68     -0.97     33.74
   8 TC/GA     -0.27     -0.23      3.47      0.68     -1.69     42.14
   9 CG/CG      0.70      0.78      3.07     -3.66      4.18     26.58
  10 GC/GC     -1.31      0.36      3.37     -2.85     -9.37     41.60
  11 CG/CG     -0.31      0.21      3.17     -0.68      6.69     33.31
****************************************************************************

Reversing the order of chains A and B in ‘355d.pdb’ as ‘355d-reversed.pdb’ and repeating the above procedure, we have the following results:

find_pair 355d-reversed.pdb 355d-reversed.bps
    # contents of file '355d-reversed.bps':
------------------------------------------------------------------
355d-reversed.pdb
355d-reversed.out
    2         # duplex
   12         # number of base-pairs
    1    1    # explicit bp numbering/hetero atoms
    1   24  0 #    1 | ....>B:..13_:[.DC]C-----G[.DG]:..12_:A<....
    2   23  0 #    2 | ....>B:..14_:[.DG]G-----C[.DC]:..11_:A<....
    3   22  0 #    3 | ....>B:..15_:[.DC]C-----G[.DG]:..10_:A<....
    4   21  0 #    4 | ....>B:..16_:[.DG]G-----C[.DC]:...9_:A<....
    5   20  0 #    5 | ....>B:..17_:[.DA]A-----T[.DT]:...8_:A<....
    6   19  0 #    6 | ....>B:..18_:[.DA]A-----T[.DT]:...7_:A<....
    7   18  0 #    7 | ....>B:..19_:[.DT]T-----A[.DA]:...6_:A<....
    8   17  0 #    8 | ....>B:..20_:[.DT]T-----A[.DA]:...5_:A<....
    9   16  0 #    9 | ....>B:..21_:[.DC]C-----G[.DG]:...4_:A<....
   10   15  0 #   10 | ....>B:..22_:[.DG]G-----C[.DC]:...3_:A<....
   11   14  0 #   11 | ....>B:..23_:[.DC]C-----G[.DG]:...2_:A<....
   12   13  0 #   12 | ....>B:..24_:[.DG]G-----C[.DC]:...1_:A<....
------------------------------------------------------------------

analyze 355d-reversed.bps
    # generate output file '355d-reversed.out', with base-pair step parameters:
****************************************************************************
    step       Shift     Slide      Rise      Tilt      Roll     Twist
   1 CG/CG      0.31      0.21      3.17      0.68      6.69     33.31
   2 GC/GC      1.31      0.36      3.37      2.85     -9.37     41.60
   3 CG/CG     -0.70      0.78      3.07      3.66      4.18     26.58
   4 GA/TC      0.27     -0.23      3.47     -0.68     -1.69     42.14
   5 AA/TT      0.08     -0.40      3.22     -1.68     -0.97     33.74
   6 AT/AT      0.01     -0.60      3.22      0.31     -2.67     32.40
   7 TT/AA     -0.17     -0.33      3.30      0.33      0.46     37.52
   8 TC/GA      0.45     -0.14      3.39      1.59      1.37     37.50
   9 CG/CG      0.14      0.59      3.00     -0.97     11.30     25.11
  10 GC/GC     -0.50      0.67      3.69     -2.85     -9.06     43.88
  11 CG/CG     -0.09      0.04      3.20      3.22      8.52     32.73
****************************************************************************

Comparing the base-pair step parameters between ‘355d.out’ and ’355d-reversed.out’, one would notice that while slide/rise/roll/twist simply switch orders, shift/tilt (the x-axis parameters) also flip their signs. On the other hand, the nucleotide serial numbers specifying base pairs (the left two columns) are identical in ‘355d.bps’ and ’355d-reversed.bps’.

Apart from explicitly swapping the two strands in PDB data file, one can simply switch around the nucleotide serial numbers generated with find_pair in order to analyze a DNA duplex based on its complementary sequence instead of the primary one. For example, starting from the same PDB file ‘355d.pdb’, we change ‘355d.bps’ to ’355d-cs.bps’ as below,

------------------------------------------------------------------
355d.pdb
355d-cs.out
    2         # duplex
   12         # number of base-pairs
    1    1    # explicit bp numbering/hetero atoms
   13   12
   14   11
   15   10
   16    9
   17    8
   18    7
   19    6
   20    5
   21    4
   22    3
   23    2
   24    1
------------------------------------------------------------------

Run analyze 355d-cs.bps, one would get exactly the same parameters in output file ’355d-cs.out’ as in ’355d-reversed.out’.

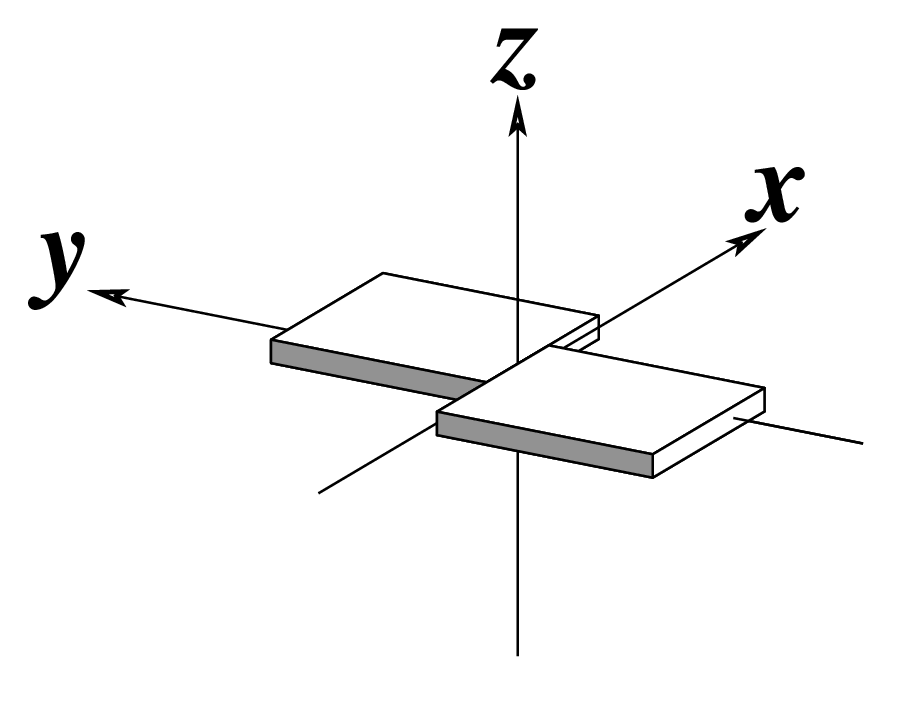
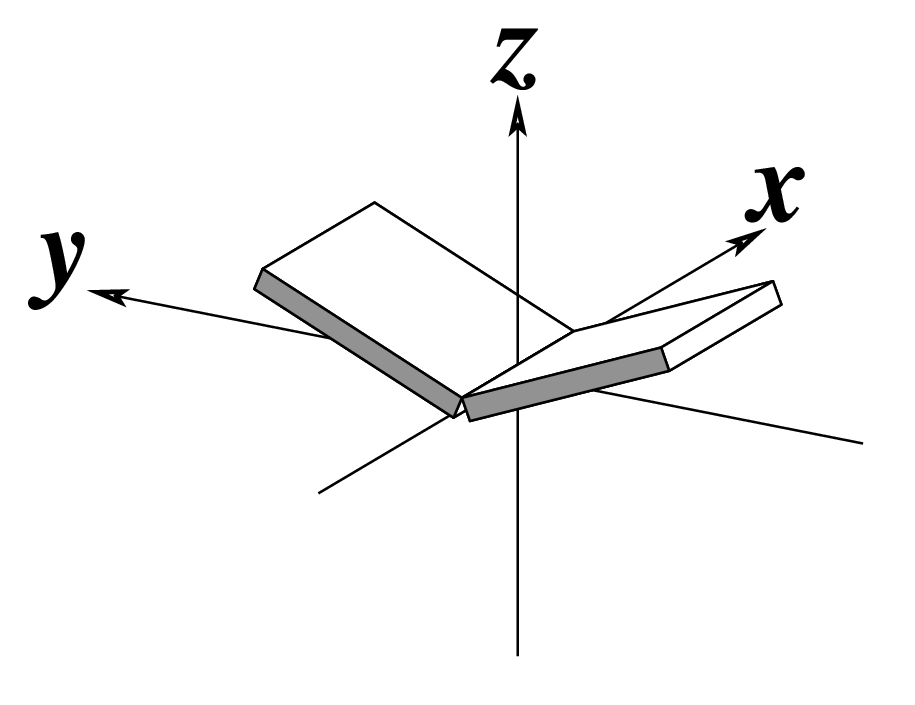
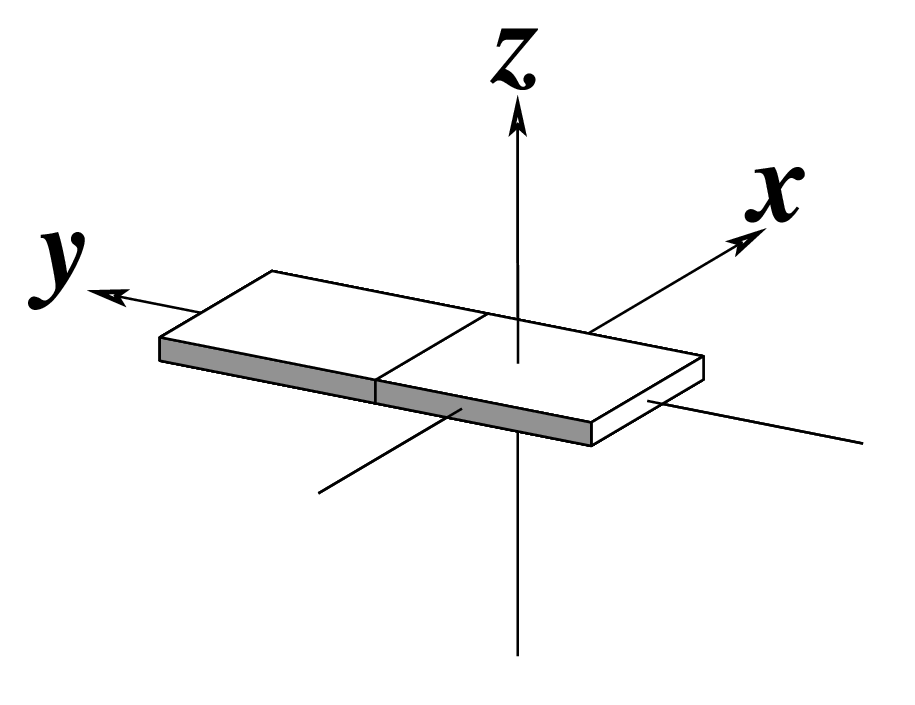
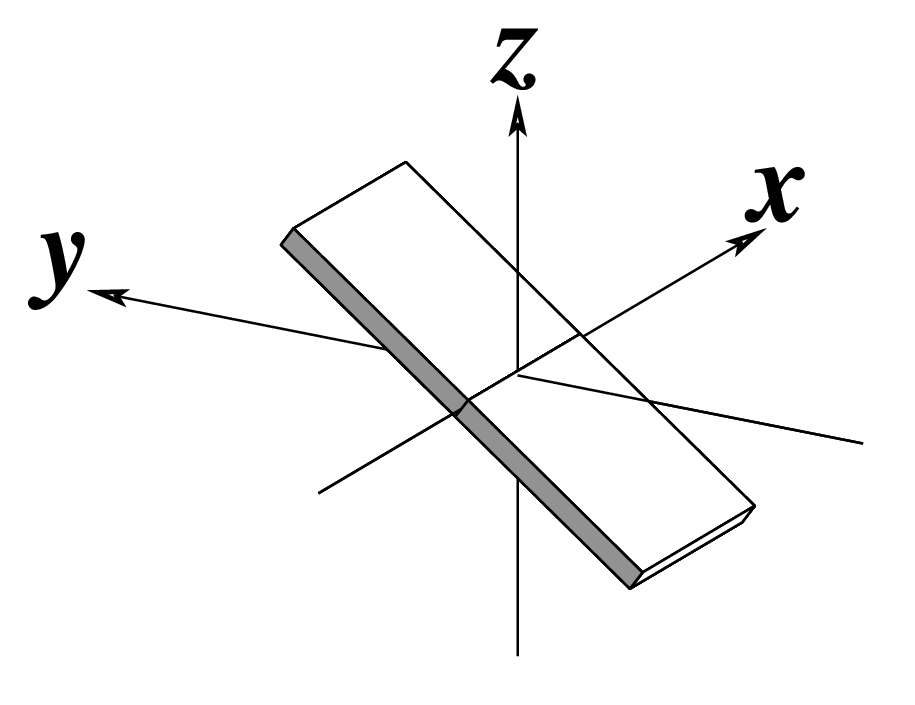
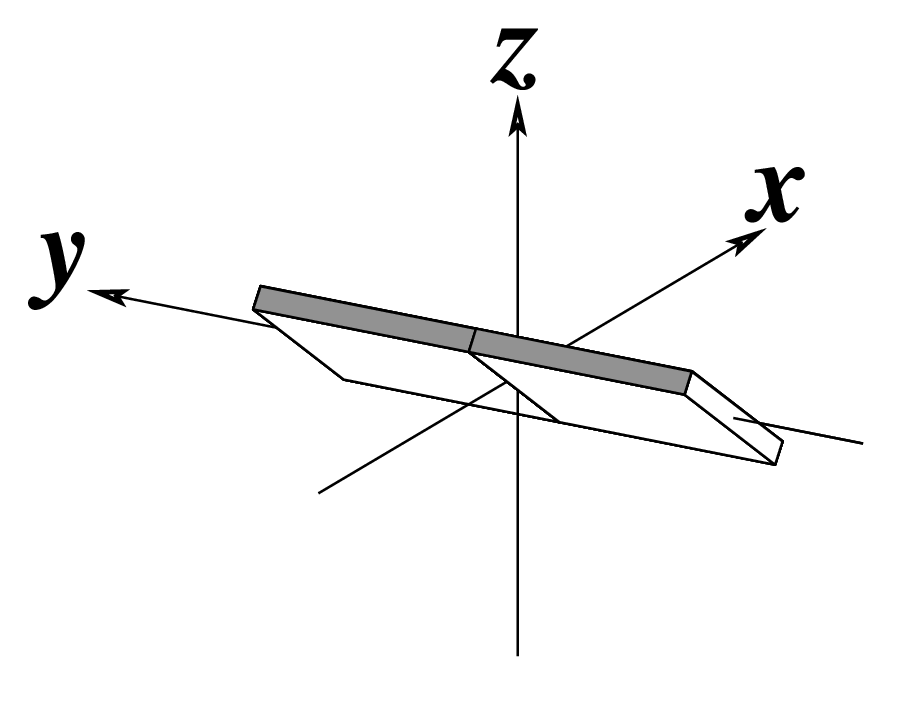
Ever since the 2003 publication of the initial 3DNA Nucleic Acids Research paper (NAR03), the schematic diagrams of base-pair parameters (see figure below) has become quite popular. Over the years, we have received numerous requests for permission to use the figure, or a portion thereof; as an example, the figure has been adopted into a structural biology textbook. In the 2008 3DNA Nature Protocols paper (NP08), we devoted the very first protocol to “create a schematic image for propeller of 45°”.

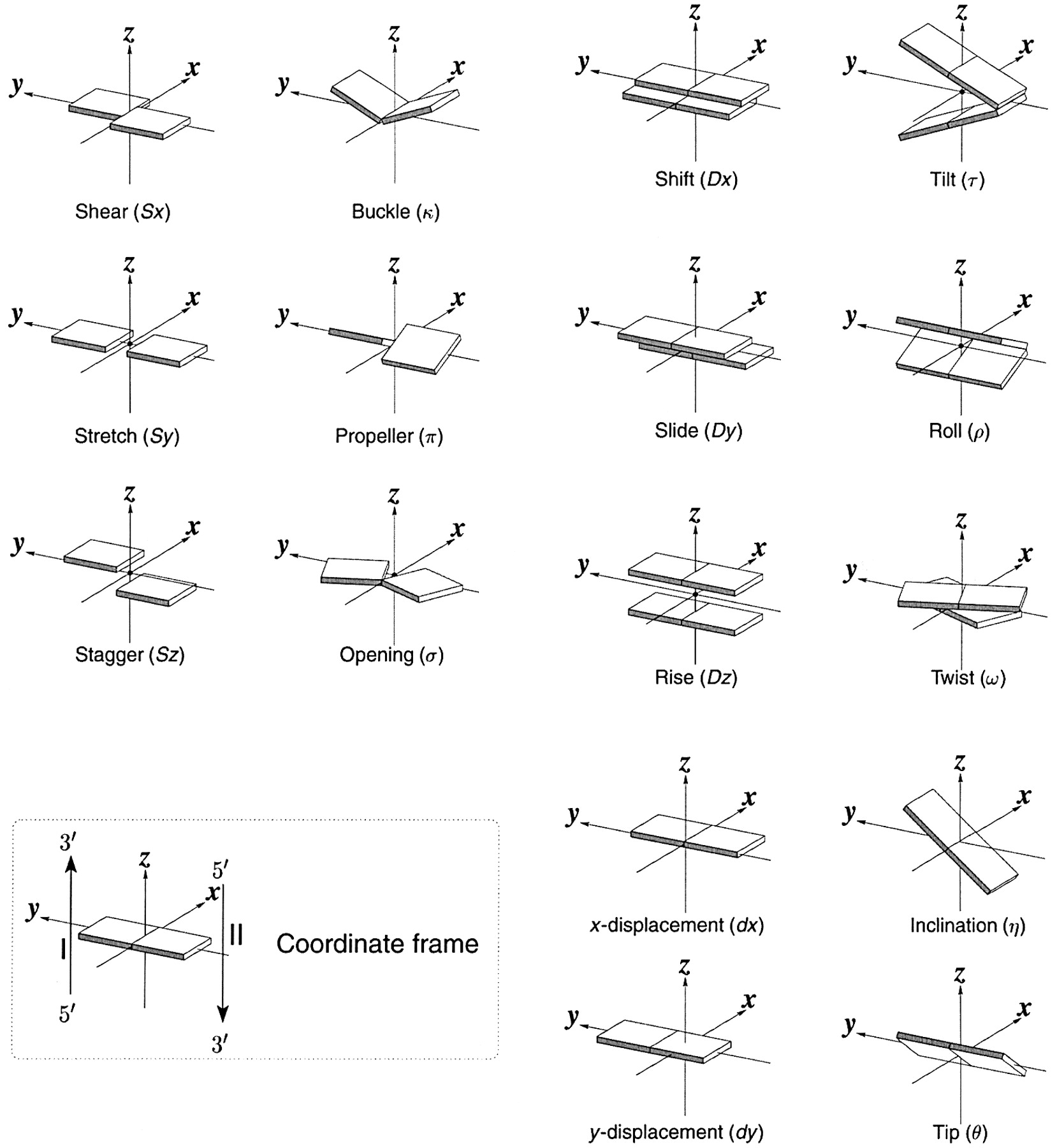
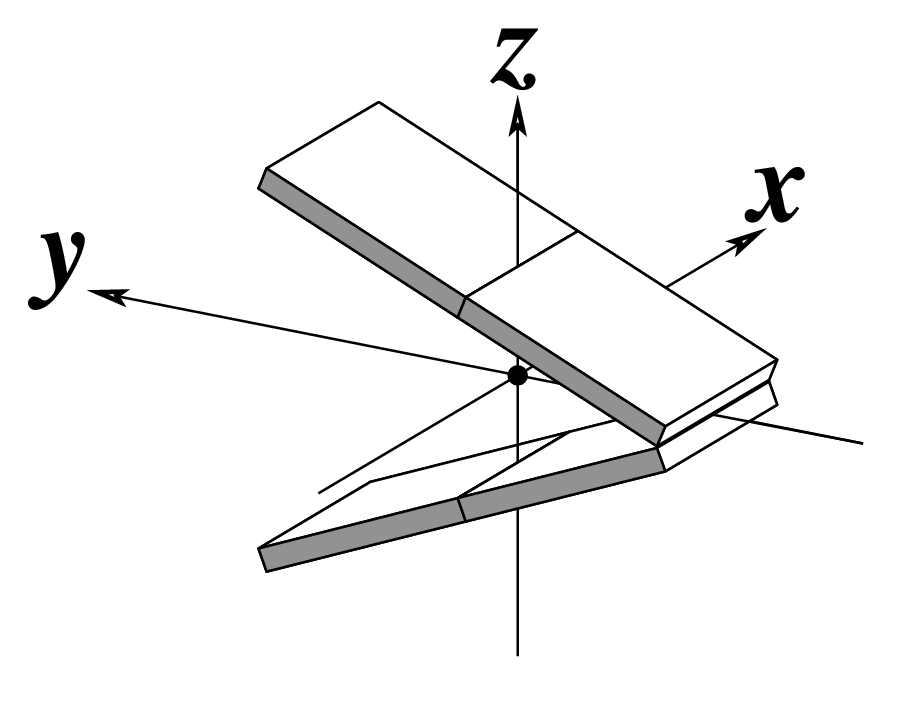
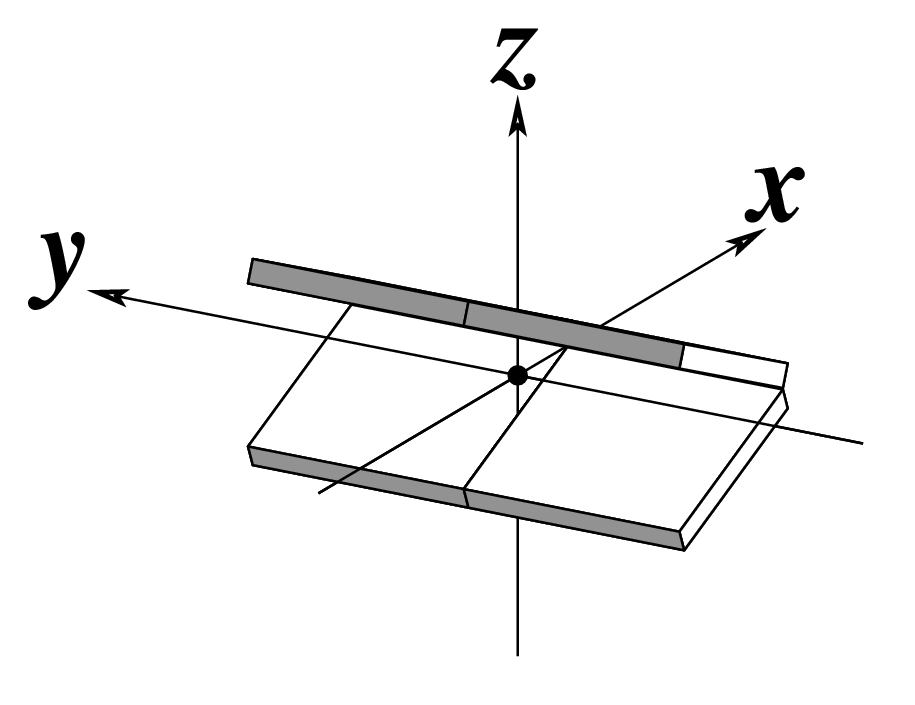
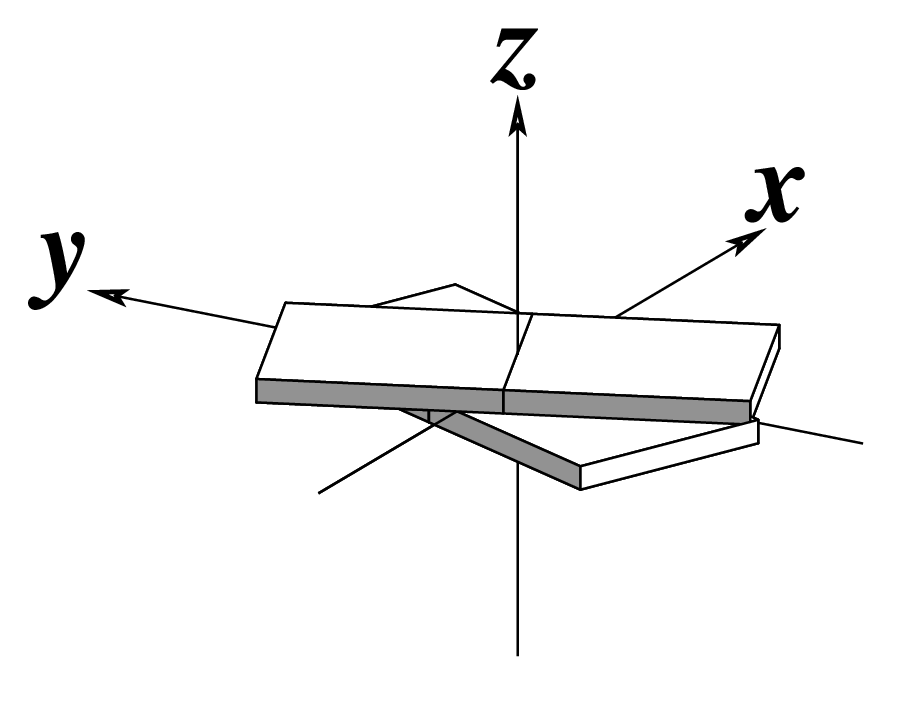
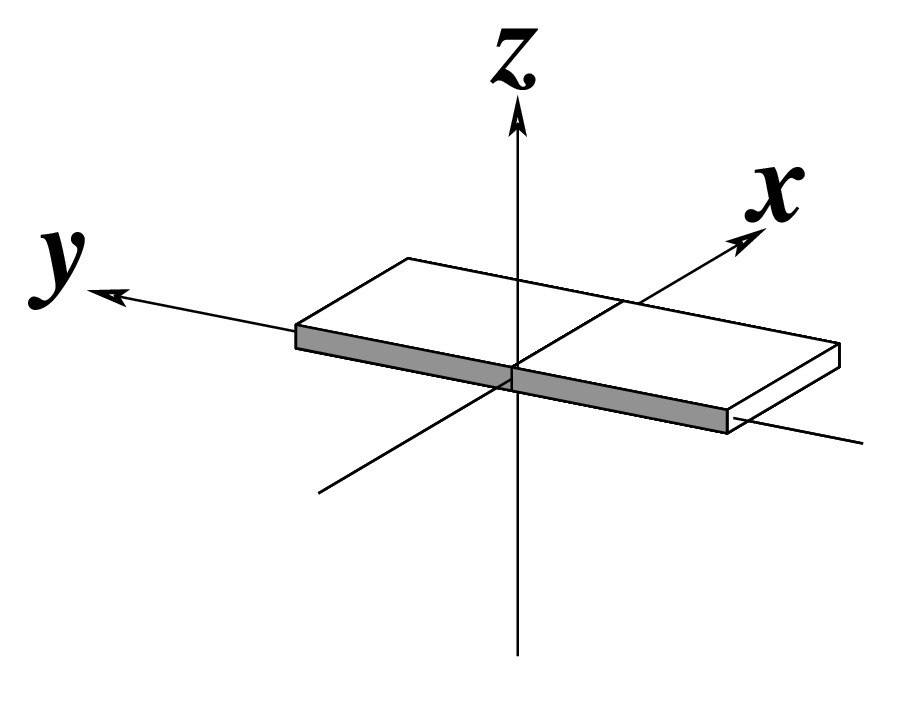
Figure legend taken from Figure 1 of NAR03: Pictorial definitions of rigid body parameters used to describe the geometry of complementary (or non‐complementary) base pairs and sequential base pair steps (19). The base pair reference frame (lower left) is constructed such that the x‐axis points away from the (shaded) minor groove edge of a base or base pair and the y‐axis points toward the sequence strand (I). The relative position and orientation of successive base pair planes are described with respect to both a dimer reference frame (upper right) and a local helical frame (lower right). Images illustrate positive values of the designated parameters. For illustration purposes, helical twist (Ωh) is the same as Twist (ω), formerly denoted by Ω (19,20) and helical rise (h) is the same as Rise (Dz).

I recall spending around two weeks to produce the above figure. Content-wise, the figure was constructed in only a short while; it was the little details that took me most of the time.

Over time, I’ve witnessed numerous versions of such schematic images in publications related to DNA/RNA structures. While looking similar, the schematics differ subtly in the magnitude, orientation and relative scale of illustrated parameters. To the best of my knowledge, only 3DNA provides a pragmatic approach to generate the base-pair schematic diagrams consistently.

To make the schematics more readily accessible, I’ve reproduced a high resolution image (in png format) for each of the 14 parameters shown above. You are welcome to pick and match the diagrams as necessary. If you use any of them in your publications, please cite the 3DNA NAR03 and/or NP08 paper(s).

Note that in the schematic diagrams below, the shaded edge (facing the viewer) denotes the minor-groove side of a base or base pair.

Shear (Sx)	Stretch (Sy)	Stagger (Sz)
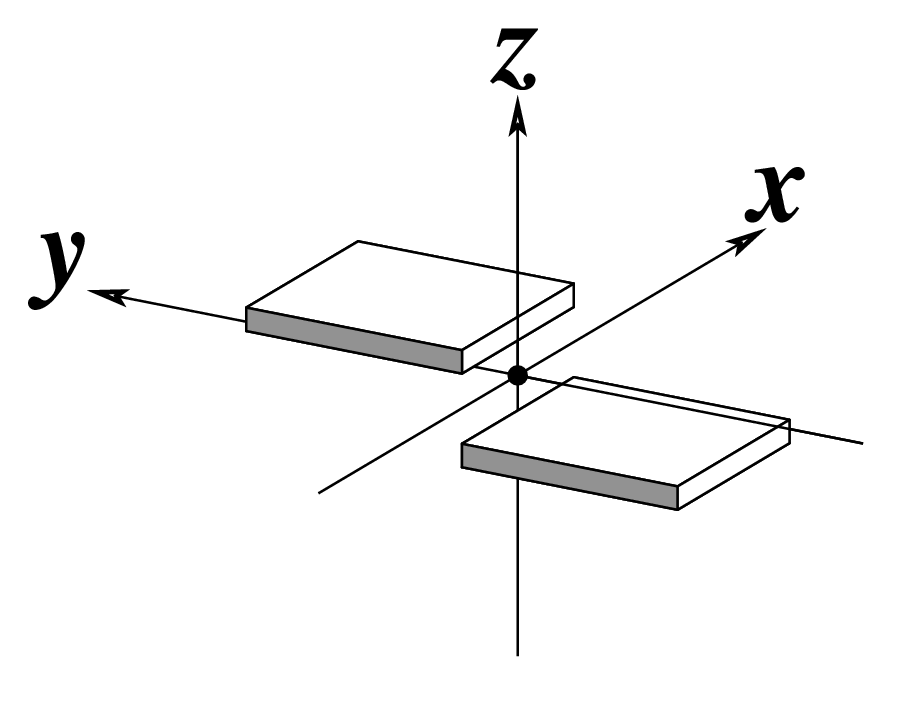Buckle (κ)	Propeller (π)	Opening (σ)
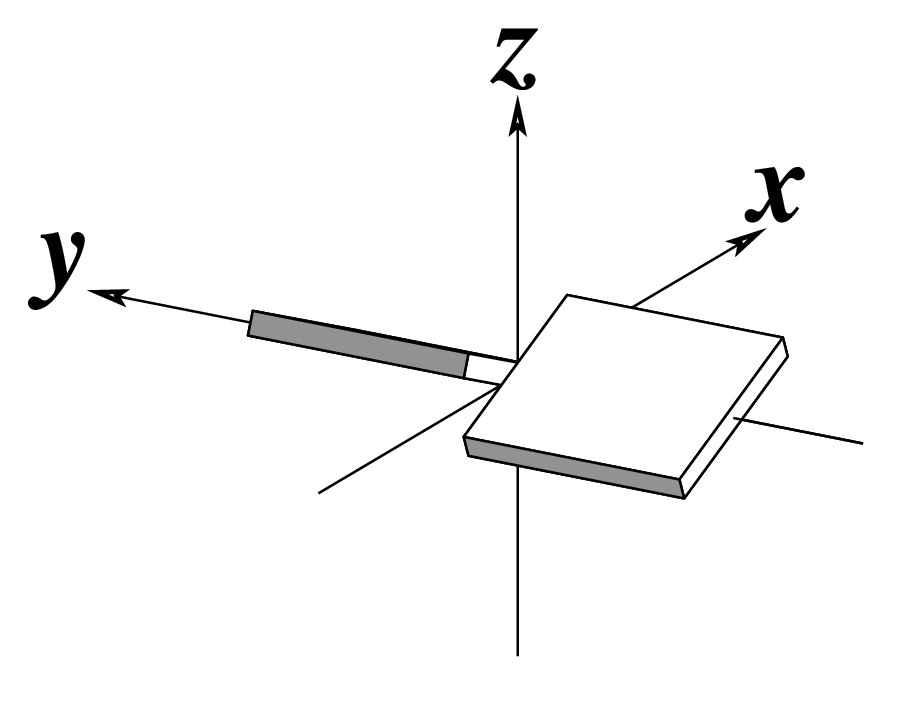
Shift (Dx)	Slide (Dy)	Rise (Dz)
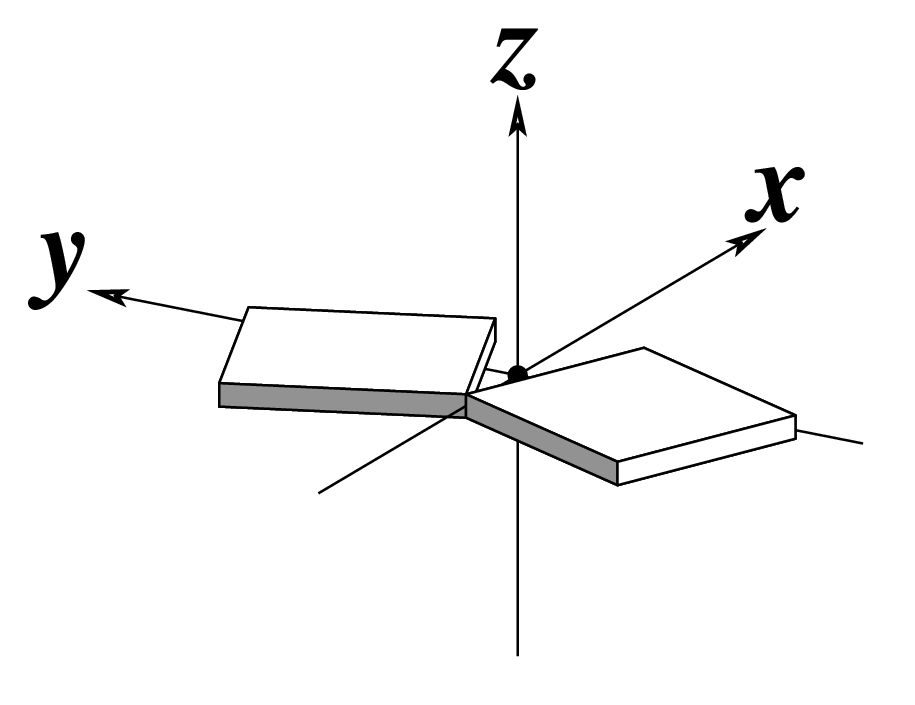
Tilt (τ)	Roll (ρ)	Twist (ω)
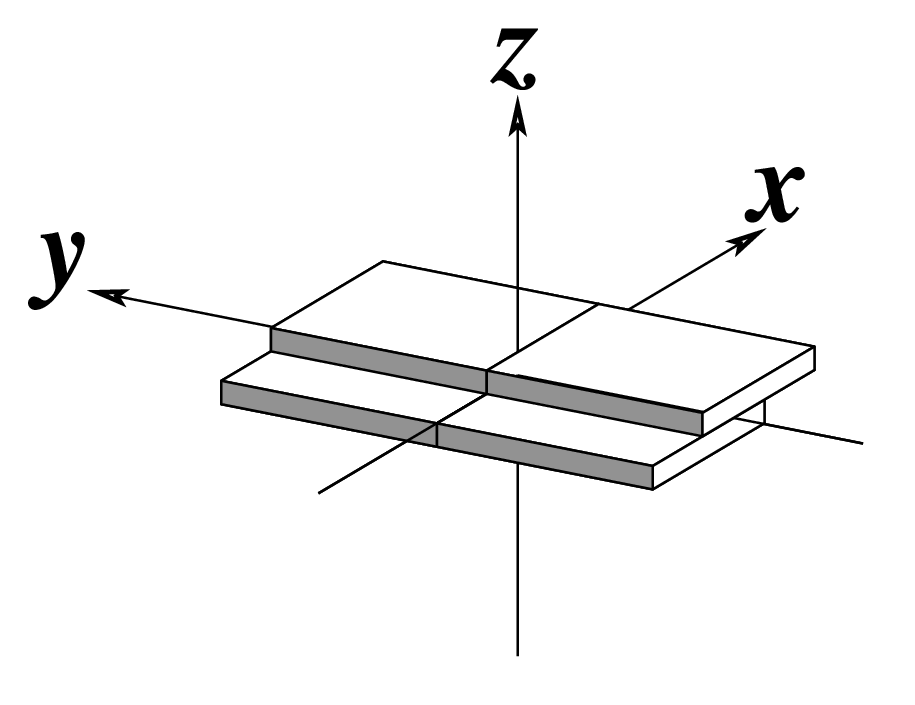
x-displacement (dx)	y-displacement (dy)	Helical Rise (h)
		As for Rise above (for illustration purpose)
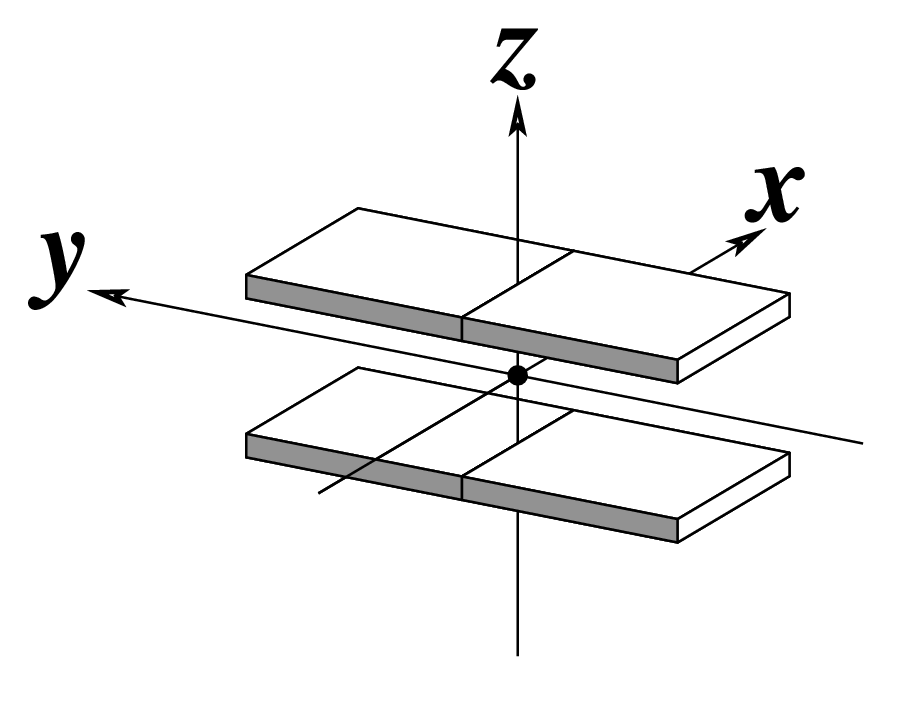
Inclination (η)	Tip (θ)	Helical Twist (Ωh)
		As for Twist above (for illustration purpose)

As of v2.1, I’ve switched from Perl to Ruby as the scripting language for 3DNA. Consequently, the Perl scripts in previous versions of 3DNA (v1.5 and v2.0) are now obsolete. I’ll only correct bugs in existing Perl scripts, but will not add any new features.

For back reference, the scripts are still available from a separate directory $X3DNA/perl_scripts, with the following contents:

OP_Mxyz*          dcmnfile*         nmr_strs*
README            del_ms*           pdb_frag*
block_atom*       expand_ids*       x3dna2charmm_pdb*
blocview.pl*      manalyze*         x3dna_r3d2png*
bp_mutation*      mstack2img*       x3dna_setup.pl*
cp_std*           nmr_ensemble*     x3dna_utils.pm

Among them, x3dna_setup.pl and blocview.pl have corresponding Ruby versions: x3dna_setup and blocview. Actually, the .pl file extension (for Perl) was added to avoid confusion with the new Ruby scripts.

Some of the functionalities have been incorporated into the Ruby script x3dna_utils:

------------------------------------------------------------------------
A miscellaneous collection of 3DNA utilities
    Usage: x3dna_utils [-h|-v] sub-command [-h] [options]
    where sub-command must be one of: 
        block_atom -- generate a base block schematic representation
        cp_std -- select standard PDB datasets for analyze/rebuild
        dcmnfile -- remove fixed-name files generated with 3DNA
        x3dna_r3d2png -- convert .r3d to image with Raster3D or PyMOL
------------------------------------------------------------------------
  --version, -v:   Print version and exit
     --help, -h:   Show this message

Along the same line, ensemble-related functionalities (for NMR or molecular dynamics simulations) have been consolidated and extended into the new Ruby script x3dna_ensemble:

------------------------------------------------------------------------
Utilities for the analysis and visualization of an ensemble
    Usage: x3dna_ensemble [-h|-v] sub-command [-h] [options]
    where sub-command must be one of: 
        analyze -- analyze MODEL/ENDMDL delineated ensemble (NMR or MD)
        block_image -- generate a base block schematic image
        extract -- extract structural parameters after running 'analyze'
        reorient -- reorient models to a particular frame/orientation
------------------------------------------------------------------------
  --version, -v:   Print version and exit
     --help, -h:   Show this message

Conceivably, C programs in 3DNA can also be consolidated. For backward compatibility, however, all existing C programs will be kept — and refined as necessary — in the current 3DNA v2.x series. As of v3.x, I’ll completely re-organize 3DNA incorporating my years of experience in programming languages and knowledge of macromolecular structures.

In 3DNA, each base pair (bp) is specified by the identity of its two comprising nucleotides (nts), and their interactions. Some examples are shown below based on the PDB entry 1ehz (the crystal structure of yeast phenylalanine tRNA at 1.93 Å resolution), with the shorthand form on the right:

....>A:...1_:[..G]G-----C[..C]:..72_:A<....  G-C
....>A:...4_:[..G]G-*---U[..U]:..69_:A<....  G-U
....>A:...9_:[..A]A-**+-A[..A]:..23_:A<....  A+A
....>A:..15_:[..G]G-**+-C[..C]:..48_:A<....  G+C
....>A:..26_:[M2G]g-**--A[..A]:..44_:A<....  g-A

Specification of a nucleotide

The nt specification string consists of 6 fields and follows the pattern below, with the number of characters in each field inside the parentheses:

modelNum(4)>chainId(1):ntNum(4)insCode(1):[ntName(3)]baseName(1)

1. modelNum(4) — the model number is up to 4 digits, right-justified, with each leading space replaced by a dot. If no model number is available, as is the case for 1ehz (and virtually all other x-ray crystal structures in the PDB), it is written as .... (4 dots).
2. chainId(1) — the chain id is 1-char long, with space replaced by underscore.
3. ntNum(4) — the nt residue number, handled as for the model number.
4. insCode(1) — insertion code, handled as for the chain id.
5. ntName(3) — the nt residue name is up to 3-char long, right-justified, with each leading space replaced by a dot.
6. baseName(1) — the base name is 1-char long, mapped from ntName(3) following $X3DNA/config/baselist.dat. Note that modified nucleotides are put in lower case to distinguish them from the canonical ones — for example, M2G to g.

For the complementary base in a bp, the order of the 6 fields is reversed — see examples above. To see the full list of nts in a PDB data file, run: find_pair -s 1ehz.pdb stdout (here using 1ehz as an example).

Specification of a base pair

The pattern of a bp is M-xyz-N, where M and N are 1-char base names (as in aforesaid field #6), and the three characters xyz have the following meaning:

• z — the sign of the dot product of the z-axes of the M and N base reference frames. It is positive (+) if the two z-axes point in similar directions, as in Hoogsteen or reverse Watson-Crick bps. Conversely, it is negative (-) when the two z-axes point in opposite directions, as in the canonical Watson-Crick and Wobble bps. See figure below:

• y — it is - if M and N are in a so-called Watson-Crick geometry (the two y-axes of the M and N base reference frames are anti-parallel, so are the two z-axes, whilst the two x-axes are parallel), e.g., the G-U Wobble pair; otherwise, *.
• x — it is - for Watson-Crick bps, otherwise, *.

By design, Watson-Crick bps would be of the pattern M-----N, Wobble bps M-*---N, and non-canonical bps M-**+-N or M-**--N. Thus by browsing through the 3DNA output, users can readily identify these three bp types.

The shortened form is represented as MzN; following aforementioned notation, it can be either M-N or M+N. The relative direction of the two z-axes is critical in effecting 3DNA-calculated bp (and step) parameters, as detailed in the 2003 3DNA NAR paper:

To calculate the six complementary base pair parameters of an M–N pair (Shear, Stretch, Stagger, Buckle, Propeller and Opening), where the two z‐axes run in opposite directions, the reference frame of the complementary base N is rotated about the x2‐axis by 180°, i.e. reversing the y2‐ and z2‐axes in Figure 2a. Under this convention, if the base pair is reckoned as an N–M pair, rather than an M–N pair, the x‐axis parameters (Shear and Buckle) reverse their signs. For an M+N pair, e.g. the Hoogsteen A+U in Figure 2b, the x2‐, y2‐ and z2‐axes do not change sign; thus all six parameters for an N+M pair are of opposite sign(s) from those for an M+N pair.

The M-N and M+N bp designation is unique to 3DNA. In combination with the corresponding 6 bp parameters (shear, stretch, stagger, buckle, propeller, and opening), 3DNA provides a rigorous description of all possible bps. This contrasts and complements with the conventional Saenger scheme and the 3-edge based Leontis/Westhof notation.

The 3DNA M-N vs M+N bp designation is base-centric, without concerning the sugar-phosphate backbone. The chi (χ) torsion angle, which characterizes base/sugar relative orientation, can be in either anti or syn conformation; thus similar backbone(S) can accommodate either M-N or M+N.

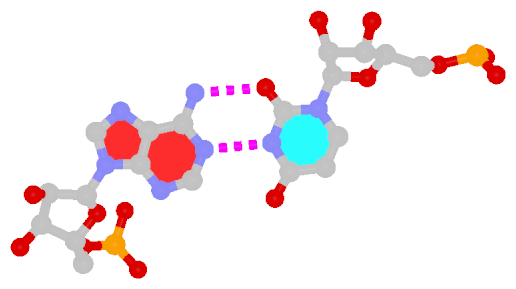
Among the findings of our 2010 Nucleic Acids Research (NAR) article titled The RNA backbone plays a crucial role in mediating the intrinsic stability of the GpU dinucleotide platform and the GpUpA/GpA miniduplex, the key is identifying the O2′(G)…O2P(U) H-bond (see figure below). As noted in a previous post What’s special about the GpU dinucleotide platform?, it was an accidental observation while I was preparing a figure for our 2008 3DNA Nature Protocols paper. Trained as a chemist, after scrutinizing the many occurrances of the GpU platforms in the large ribosomal subunit of Haloarcula marismortui (PDB entry 1jj2), I had no doubt that it is an H-bond. Yet, behind the scene, things were never that straightforward: if it is indeed an H-hbond as we’ve claimed, how could it have been missed altogether by the RNA structural biology community?

Anticipating the potential questions that could be raised by the reviewers, we were extremely careful in characterizing the O2′(G)…O2P(U) H-bond:

• It is formed between the hydroxyl group (donor) of G and a non-bridging phosphate oxygen atom (O2P, acceptor) of U.
• The distance between O2′(G) and O2P(U), 2.68 ± 0.14 Å, is perfect for an H-bond.
• I queried the Cambridge Structure Database for hydroxyl-phosphate H-bonds with similar relative geometry and chemical identity. We found a case in the phospholipid lysophosphatidyl-ethanolamine, where this type of H-bond is highlighted in the abstract: The free glycerol hydroxyl group forms an intramolecular hydrogen bond with a phosphate oxygen and thus affects the conformation and orientation of the head group.
• I also performed a survey of potential O2′(i)…O2P(i+1) H-bonds within dinucleotides regardless of platform configuration, and detected 1186 such pairwise interactions within a distance cutoff of 3.3 Å in RNA crystal structures of 2.5 Å or better resolution.

Careful as we were, we still failed to convince reviewer #3 of our manuscript, which was originally submitted to the RNA journal and finally rejected following the second round of review. Here is an excerpt related to the O2′(G)…O2P(U) H-bond from reviewer #3’s comment:

The first main concern is that the “new” H-bond interaction that the authors propose as an explanation for the greater occurrence of GU platforms versus di-nucleotide combinations does not make much sense on a fundamental chemical and stereo-chemical point of view. Unless the whole community of chemists and biochemists agree to redefine what an H-bond is, the fact that the 2’OH (i) atom is at 2.68 Å from the O2P atom cannot be the only criteria for an H-bond. In fact, if the authors are the first to mention this H-bond, it is because none of the scientists working in RNA structural biology would have considered this to be an H-bond interaction at the first place! H-bonds are known to be very directional. The O2’-H bond should be aligned with one of the electron doublets of O2P to be able to form a proper H-bond. Acceptable variation could be 20° to 30° degree with respect of a straight H-bond interaction, not 90°! The unique paper that the authors cite for justifying their claim cannot be used as a reference. If the authors want to justify that the close proximity of the 2’OH(i) and O2P is the important factor that contributes to preference of GU platforms versus other platforms, they should undergo quantum mechanics calculations to demonstrate it.

This review is so critical that I saw no point in arguing with it — I certainly have neither the power to “redefine what an H-bond is” nor the expertise to perform quantum mechanics (QM) calculations to validate the O2′(G)…O2P(U) H-bond or otherwise. What is compelling to me about the GpU story from the very beginning is that once this sugar-phosphate H-bond is acknowledged, every other parts of our NAR paper follow naturally and logically. Leaving the chicken or the egg issue alone, our work provides a novel perspective about GpU platform’s predominance, the formation of the bulged-G or loop-E motif, the evolutionary co-occurrence of GpUpA and GpA in the GpUpA/GpA miniduplex, and the extreme conservation of GpU observed at most 5′-splice sites. Put another way, we connect the dots to form a coherent picture that is easily understandable to biologists and chemists.

Luckily, after being re-submitted to NAR, the paper was quickly accepted for publication and even selected as a featured article! As another nice surprise, shortly after it was available online as an Advance Access paper, I received an email from Jiri Sponer. Thereafter, we collaborated on a follow-up paper titled Understanding the Sequence Preference of Recurrent RNA Building Blocks Using Quantum Chemistry: The Intrastrand RNA Dinucleotide Platform. While not unexpected, the results of the state-of-the-art QM calculations were nevertheless reassuring:

The mixed-pucker sugar–phosphate backbone conformation found in most GpU platforms, in which the 5′-ribose sugar (G) is in the C2′-endo form and the 3′-sugar (U) in the C3′-endo form, is intrinsically more stable than the standard A-RNA backbone arrangement, partially as a result of a favorable O2′···O2P intraplatform interaction. Our results thus validate the hypothesis of Lu et al. (Lu, X.-J.; et al. Nucleic Acids Res. 2010, 38, 4868–4876) that the superior stability of GpU platforms is partially mediated by the strong O2′···O2P hydrogen bond. …… In contrast, we show that the dinucleotide platform is not properly described in the course of atomistic explicit-solvent simulations. Our work also gives methodological insights into QM calculations of experimental RNA backbone geometries. Such calculations are inherently complicated by rather large data and refinement uncertainties in the available RNA experimental structures, which often preclude reliable energy computations.

So, the O2′(G)…O2P(U) H-bond is more than likely to be real; at least some other scientists working in RNA structural biology do share our view.

See also: What’s special about the GpU dinucleotide platform?

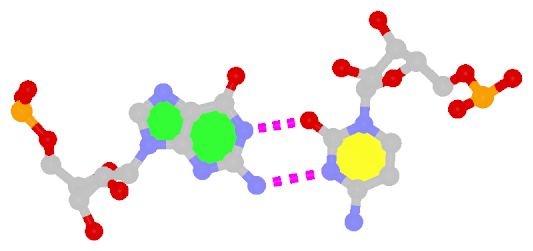
While the Watson-Crick (WC) base pairs (bps) are best-known and most abundant in nucleic acid structures (including RNA), the so-called reverse WC bp variants have received little attention. In the well-established Saenger scheme (see figure below), there are 28 possible bps for A, G, U(T), and C in their cononical (keto- and amino-) tautomeric forms and involving at least two H-bonds. The reverse A·T/U and G·C WC pairs are asymmetric, and are numbered XXI and XXII respectively (middle of right-hand side in the figure below).

In 3DNA, the WC bps are of type M–N and listed as A–T and G–C, consistent with the conventional notation. The reverse WC bps, on the other hand, are of type M+N and listed as A+T and G+C; the ‘+’ signifies the parallel z-axes of the two base reference frames, therefore their dot product is positive (see figure 2 in post Hoogsteen and reverse Hoogsteen base pairs).

As of this writing, a Google search of the phrase “reverse Watson Crick base pair” does not come up with anything informative — the top hit is the Jena Library page titled Nucleic Acid Nomenclature and Structure showing the same set of 28 possible bps only with explicit base chemical structures, as compiled by Tinoco Jr. et al. (1993).

However, once I look into this special type of bps, a quick search in PDB entry 1jj2, the Haloarcula marismortui large ribosomal subunit solved at 2.4 Å resolution, revealed nine reverse WC bps as shown below:

 __U.U..0.205._   __A.A..0.437._   [U+A]
 __C.C..0.1186._  __G.G..0.1190._  [C+G]
 __C.C..0.1377._  __G.G..0.1683._  [C+G]
 __C.C..0.1856._  __G.G..0.1873._  [C+G]
 __A.A..0.2054._  __U.U..0.2648._  [A+U]
 __U.U..0.2109._  __A.A..0.2467._  [U+A]
 __A.A..0.2301._  __U.U..0.2306._  [A+U]
 __A.A..0.2321._  __U.U..0.2378._  [A+U]
 __C.C..0.2510._  __G.G..0.2564._  [C+G] 

The following figure shows a representative reverse WC A+U bp (0.A437 with 0.U205, top), and a representative reverse WC G+C bp (0.G1683 with 0.C1377, bottom). For easy comparison, the two reverse WC bps are orientated in the reference frames of A and G, respectively.

In future releases of 3DNA, presumably starting from v2.2, we plan to provide a new component to classify bps according to the Saenger scheme, the Leontis/Westhof notation, and the geometric parameter-based strategy. Overall, the three bp classification methods are complementary in functionality, but with increased sophistication and applicability.