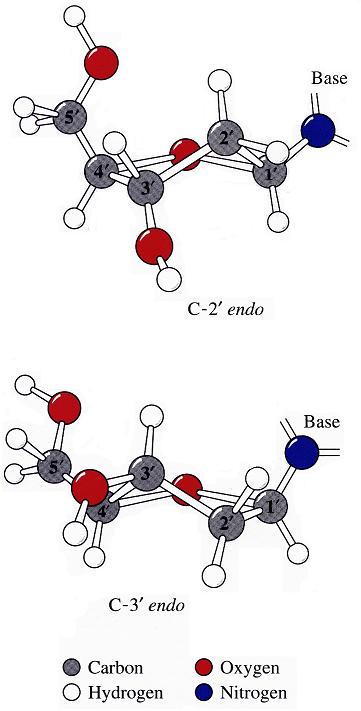
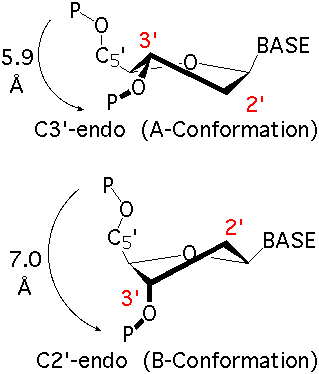
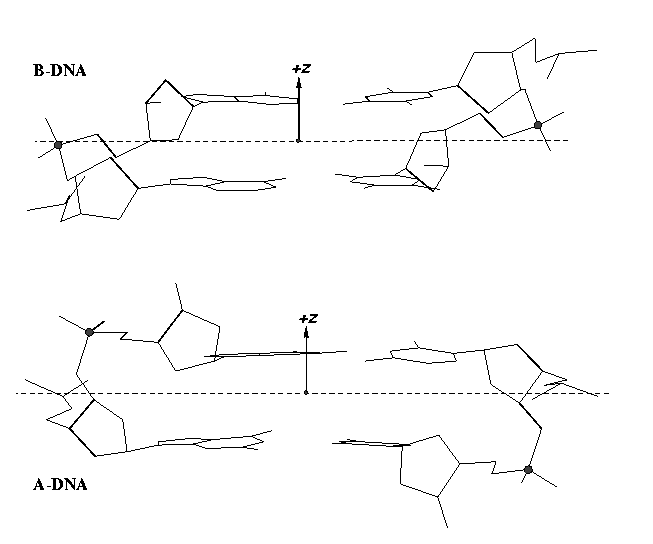
The sugar puckers in DNA/RNA structures are predominately in either C3′-endo (A-DNA or RNA) or C2′-endo (B-DNA; see Figure below, left), corresponding to the A- or B-form conformation in a duplex. In these two sugar conformations, the distance between neighboring phosphorus (P) atoms and the orientation of P relative to the sugar/bases are also dramatically different (figure below, right).

Recently, I carefully re-read some articles on RNA backbone conformation by Richardson et al., including:

• RNA backbone is rotameric (PNAS 2003)
• RNA backbone: consensus all-angle conformers and modular string nomenclature (RNA 2008)
• MolProbity: all-atom structure validation for macromolecular crystallography (Acta Crystallogr D Biol Crystallogr. 2010)
• PHENIX: a comprehensive Python-based system for macromolecular structure solution (Acta Crystallogr D Biol Crystallogr. 2010)

I became intrigued by one of their observations: i.e., the correlation between the sugar pucker and a simple distance parameter:

C3′-endo and C2′-endo sugar puckers are highly correlated to the perpendicular distance between the C1′–N1/9 glycosidic bond vector and the following phosphate: > 2.9 Å for C3′-endo and < 2.9 Å for C2′-endo. (p.16 from the MolProbity paper).

Out of curiosity and for a better understanding of this correlation, I played around with some sample cases both visually and numerically. Overall, this involves a simple geometric calculation, i.e., the shortest distance from a point to a line in three-dimensional space. Given below is the Octave/Matlab script for calculating the distances for G175 and U176 of PDB entry 1jj2 (the large ribosomal subunit of Haloarcula marismortui):

function d = get_p3_nc_dist(P3, C1, N)
    C1_N = N - C1;               # vector from C1′ to N
    nv_C1_N = C1_N / norm(C1_N); # normalized vector
    C1_P3 = P3 - C1;             # vector from C1′ to P3
    proj = dot(C1_P3, nv_C1_N);
    d = norm(C1_P3 - proj * nv_C1_N);
end

## G175
P3 = [70.104 112.366  44.586];
C1 = [73.017 109.666  45.304];
N9 = [74.445 109.380  45.288];
d1 = get_p3_nc_dist(P3, C1, N9)  # 2.2 Å -- C2′-endo

## U176
P3 = [66.871 116.402  46.804];
C1 = [68.213 112.454  49.279];
N1 = [69.678 112.480  49.438];
d2 = get_p3_nc_dist(P3, C1, N1)  # 4.6 Å -- C3′-endo

The GpU dinucleotide used in the above example forms a platform (see figure below), where the sugar of G175 adopts a C2′-endo conformation, and that of U176 C3′-endo. Indeed, the distance for G175 is 2.2 Å (< 2.9 Å); whilst the value for U176 is 4.6 Å (> 2.9 Å).

Note that the Richardson et al. articles focus on the RNA backbone, without paying attention to the base (pair) geometry. The 3DNA Zp parameter, which is the mean z-coordinate of the two P atoms in the mean reference frame of a dinucleotide step (see figure below), has been readily adapted to single-stranded RNA structures. For example, the vertical distances of the 3′ P atoms to the G175 and U176 base planes are 1.9 Å and 4.4 Å, respectively. Since base planes and the P atoms are the two most accurately located entities in a given nucleic acid structure, the nucleotide-based Zp variant is presumably more robust and discriminative than the distance from P to the glycosidic bond.

This new single-stranded based “Zp” parameter is available as of 3DNA v2.1.